The (deterministic) Allen-Cahn equation with Neumann boundary conditions is given by

$\begin{align*}\frac{\partial u}{\partial t} = \frac{1}{2} \frac{\partial^2 u}{\partial x^2} + [u-u^3] \;\;\;&\mathrm{in}\;\;\; \Omega\times (0,T)\\\frac{\partial u}{\partial \nu} = 0 \quad \;\;\;&\mathrm{on}\;\;\partial \Omega\times(0,T)\end{align*}$

The equation is scaled here so that represents the width of the interface between two different media. It is the gradient flow of the Ginzburg-Landau functional

$\displaystyle J(u) = \int_{\Omega}\left\{\frac{1}{2}|\nabla u|^2 + \frac{1}{4\varepsilon^2}(u^2-1)^2\right\}\,dx$

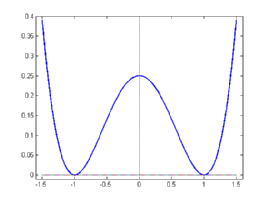
from where it follows that the desired states of the system are $\pm 1$. We think of $\pm 1$ as labelling the two different media separated by the interface.

We observe that the term $u-u^3$ is the derivative of a symmetric double-well potential as shown in the picture.

The limit $\varepsilon \rightarrow 0$ is called the sharp interface limit. It is well known that in the sharp interface limit the interface evolves according to motion by mean curvature, as shown in the animations below, which we did using the DUNE environment for C++.

For the animation below we used a randomly generated initial condition.

You may now wish to learn more on the stochastic Allen-Cahn.