Training Sets

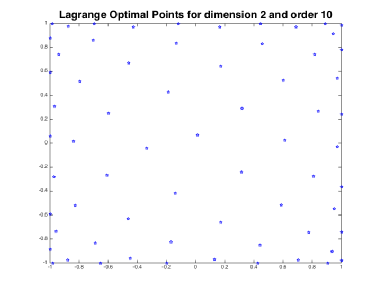
Lagrange Optimal points

Our first candidate for a training set are the Lagrange optimal points which are based on the Lagrange characteristic polynomials.

Let $\Pi_\beta^K=\{\chi:\mathbb{R}^K\to \mathbb{R}:\chi \text{ polynomial with } \text{deg}(\chi)\leq \beta\}$ be the set of polynomials on $\mathbb{R}^K$ with total degree at most $\beta$ and let $q=\dim(\Pi_\beta^K)=\binom{\beta+K}{K}$ . For $X_{\beta,K}=\{\xi_j\}_{j=1}^q\subset\Gamma$ consider $\{l_n\}_{n=1}^q$ , the Lagrange characteristic polynomials, defined so that

$l^n(\xi_j)=\delta_{nj}, n,j\in\{1,\ldots,q\}$ which form a basis of $\Pi_\beta^K$ . They can be written in terms of Vandermonde determinants,

$l^n(x)=\frac{\det[V(\xi_1,\ldots,\xi_{n-1},x,\xi_{n+1},\ldots, \xi_q)]}{\det[V(\xi_1,\ldots,\xi_q)]}, \quad n=1,\ldots,q,$

where $V\in\mathbb{R}^{q\times q}$ is such that $(V(\lambda_1,\lambda_2, \ldots,\lambda_q))_{jn}=l^n(\lambda_j)$ . Recall that the Lebesgue constant $\lambda_{q,K}$ of $X_{\beta,K}$ is defined by,

$\lambda_{q,K}:= \max_{x\in\Gamma} \sum_{n=1}^q|l^n(x)|.$

We are interested in the solutions of the following optimization problem,

$X^*_{\beta,K}=\underset{\{\xi_j\}_{j=1}^q}{\arg\min}\max_{x\in\Gamma} \sum_{n=1}^{q}|l^{n}(x)|.\quad (3)$

These solutions constitute the definition of the Lagrange optimal points.

Lagrange optimal points

Clenshaw-Curtis points

Consider the $N$ -th degree Chebyshev polynomial $T_N(x)$ defined by $T_N(cos(\theta))=cos(N\theta)$ . The Gauss-Chebyshev-Lobatto points (of degree $N$ ) are the extrema in $[-1,1]$ of $T_N(x)$ . They are given by the explicit formula:

$x_n=cos\bigg(\frac{n\pi}{N}\bigg) \smallskip n=0,\ldots,N.$

The Clenshaw-Curtis points are the nested subsequence of such points with $N(i)=2^{i-1}+1$ $(i.e. \{x_n\}_{1 \le n \le N(i)} \subset \{x_n\}_{1 \le n \le N(i+1)})$

A property of the Clenshaw-Curtis points that can be easily deduced from the explicit formula above is the asymptotic (for $N$ large) clustering of points near the boundary (i.e. near -1 and 1).

Clenshaw-Curtis (Tensor Product)

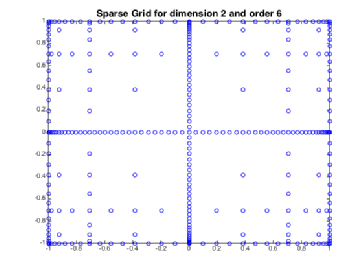
Sparse Grids

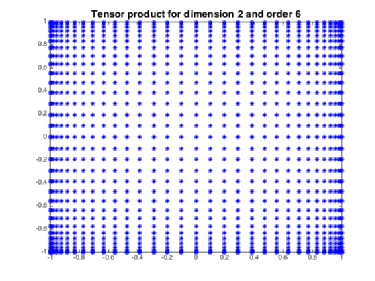
Previously we discussed the one dimensional Clenshaw-Curtis points and now we would like to go to an arbitrary dimension $K >$ 1. As soon as we try that we run into the Curse of Dimensionality: If we took the full tensor product of $N$ one dimensional points we end up with $N^K$ points in $K$ dimensions which is far too big a number for numerical schemes. The technique of Sparse Grids allows us to overcome this problem.

We start off with $N$ one dimensional points $\{x_1,\dots x_N\}$ . We would like to build a collection $H^{s}_{K,q}$ of $K$ -dimensional points, our sparse grid. Let $i=(i_1,\ldots,i_K)$ be a multi-index and consider the norm $|i|_{l_1}= \Sigma_{k=1}^{K}i_k$ and let $q \geq K.$

Take a nested family of collections of points $\{\Theta^{j}\}$ so that

$\Theta^{j} \subset \{x_1,\dots x_N\}$ for all $j$ , $\Theta^{j} \subset \Theta^{l}$ if $l>j$ and $|\Theta^{j}|=2^{j-1}+1.$

Now define the sparse grid in $K$ dimensions as follows,

$H_{K,q}^s= \underset{q-K+1 \leq |i|_{{l}_{1}} \leq q}{\bigcup} \big( \Theta^{i_1} \times \ldots \times \Theta^{i_K} \big).$

One should note that even though the actual points in the sparse grid depend on how we chose the nested family $\{\Theta^j\}$ , the cardinality of the sparse grid is independent of this choice.

Sparse Grid

Other points that we have used as training sets are :

Uniform Grid points.
Random points.