Stochastic Finance
Authors: Chin Lun,Matthew Thorpe, Abhishek Shukla
Supervisors: Vassili Kolokoltsov, Aleksandar Mijatovic
Stochastic finance is concerned with modelling the pricing behaviour of different assets, and the securities based on them, using methods from the theory of stochastic processes and stochastic analysis. To get useful information about the market behaviour one requires powerful computational methods which can analyse the mathematical models in real time. The aim of this project is to describe a variety of techniques to calculate the price of an option. We model the price of the underlying asset with a stochastic jump diffusion process. We then approximate the process by a Markov chain. Each method uses the transition rate matrix (Q-matrix) of the approximating Markov chain to estimate the price of the option.
Up-and-in call Option
An option is a type of derivative securities i.e. a security derived from the underlying asset. A call option gives the holder of the option the right but not the obligation to buy a certain fixed amount of an asset at a predefined strike price \(K\) before some time \(T\) known as the maturity or expiry time. A put is defined similarly except the holder of the option have the choice to sell an asset instead of buying it. A European option is where the option can only be exercised at expiry while an American option can be exercised anytime before maturity.
A more "exotic" type of option is the European up-and-in call option which is an example of a knock-in barrier option. . Unlike the simpler vanilla European and American options this option is path dependent as it can only be exercised if the stock price hits a certain level \(H\) before the maturity of the option.
At some prescribed expiry \(T\) the buyer has an agreement to buy the stock for a strike price \(K\) if the value of the stock is above \(K\) at expiry and at some point before expiry the stock crossed some barrier \(H\). However, if the stock price never crosses the barrier then the buyer may be entitled to a rebate. Compare this to a vanilla option where we need only know the value of the stock at expiry in order to evaluate the option.
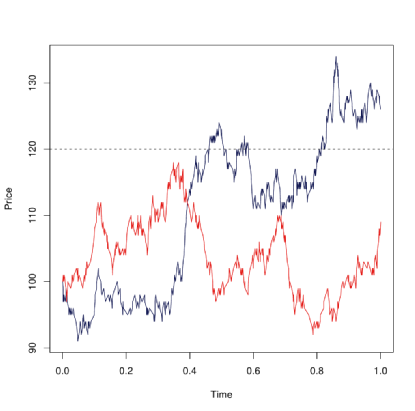
The above figure shows two stock prices where one of them (red) never hits the barrier (dotted line) during the period \([0,1]\) and the other (blue) crosses it at some point during the same period. We will mainly consider this type of option in the subsequent sections since the other barrier options such as the up-and-out, down-and-in and down-and-out etc can be priced in a similar manner.
Below is an overview of the material that can be found on this website.
Here a jump-diffusion model is described and an outline of the numerical method for pricing barrier options is given.
A modification to the sampling method is given here.
An example of a stochastic volatility model is described as well as the method to discretise and approximate the model by a Markov chain.
A more theortical approach to pricing the option is presented in the setting of a geometric Brownian motion. The formula for the PDF of the payoff of a up-and-in call option is derived under this setting.
Acknowledgements
We acknowledge and thank the help of our supervisors.
We would also like to acknowledge the funding body EPSRC and the support from MASDOC CDT.
