3rd Year PhD
Below is given a summary of the work undertaken in the third year of my PhD
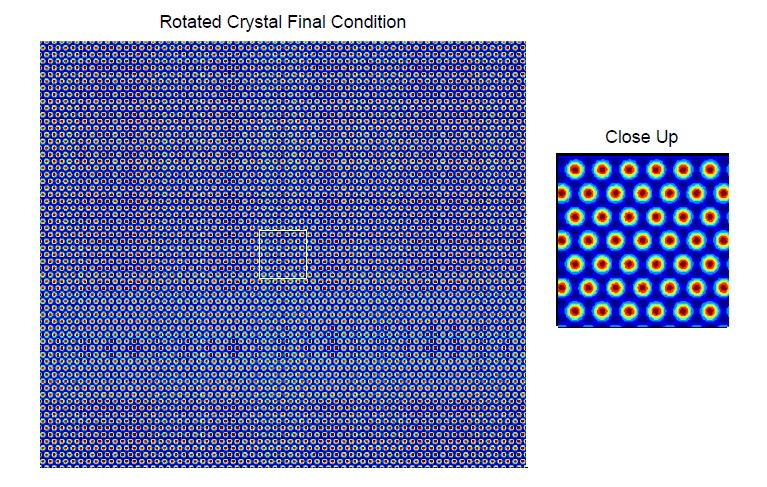
We wish to simulate some relatively realistic stitutions. We start with random initial conditions on a unit cell and run the trust region algorithm until the periodic solution is generated. We then generate a 64x64 lattice by taking 64 units cells along the x-direction and 32 unit cells in the y-direction. We then rotate a central circle of diameter one by \( \frac{\pi}{6} \). This is shown below.

We then run the three algorithms described until the norm of the gradient is small and obtain the final condition of the lattice shown below.
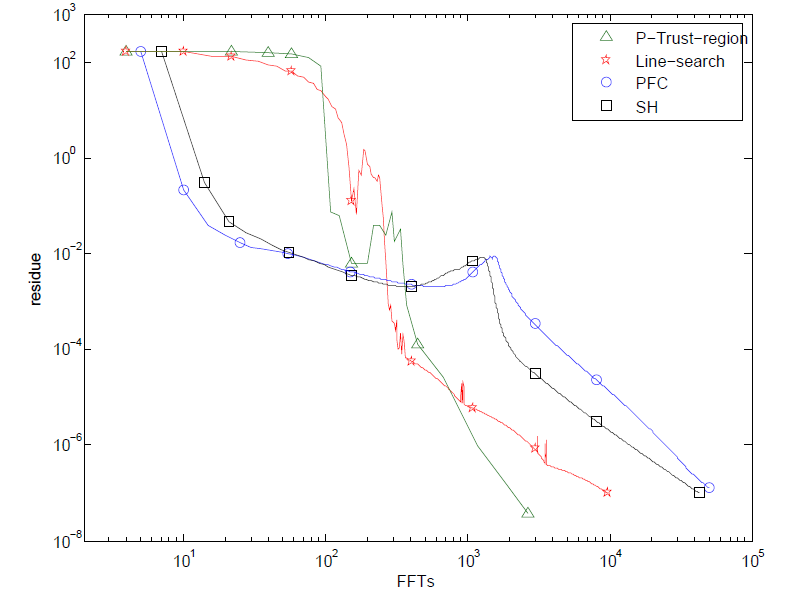
The rate of reduction of the residue for the rotated crystal, is given. Both axes are given on a logarithmic scale. This seems to demonstrate that our line-search method is quicker then the convex-concave splitting method.
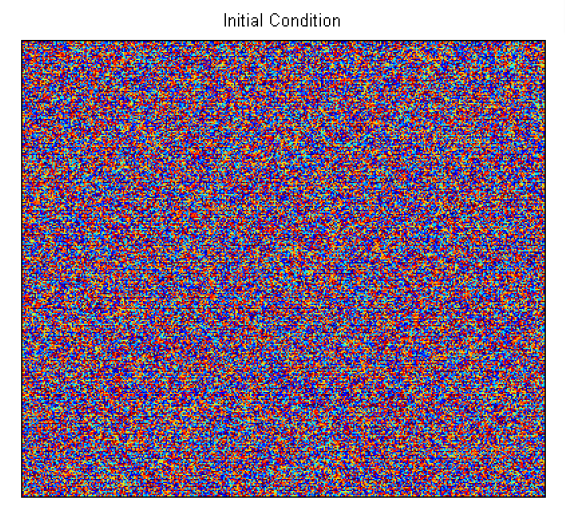
We start with the same size domain as in the section above and fillit with random initial conditions given by
\( u_0(x,y) = \textrm{rand}(x,y) + \bar u \)
This is shown in the diagram below.
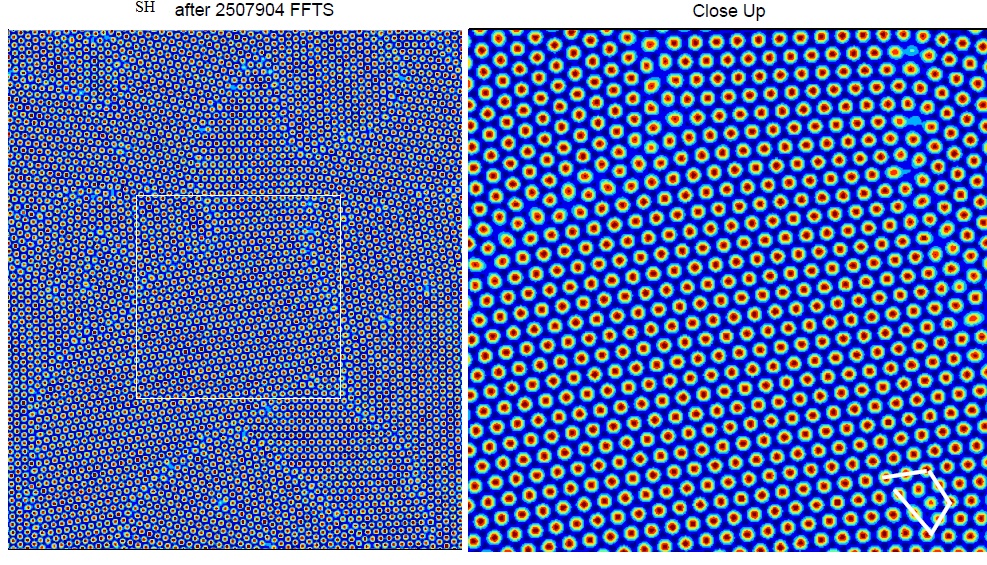
We then run our algorithms for a long time. In the line-search case we obtain the lattice as above. We give diagrams of the other three methods below where the number of FFTs taken to reach this situation is listed at the top. In all three cases we obtain grain boundaries and isolated dislocations where the dislocations are highlighted in white.
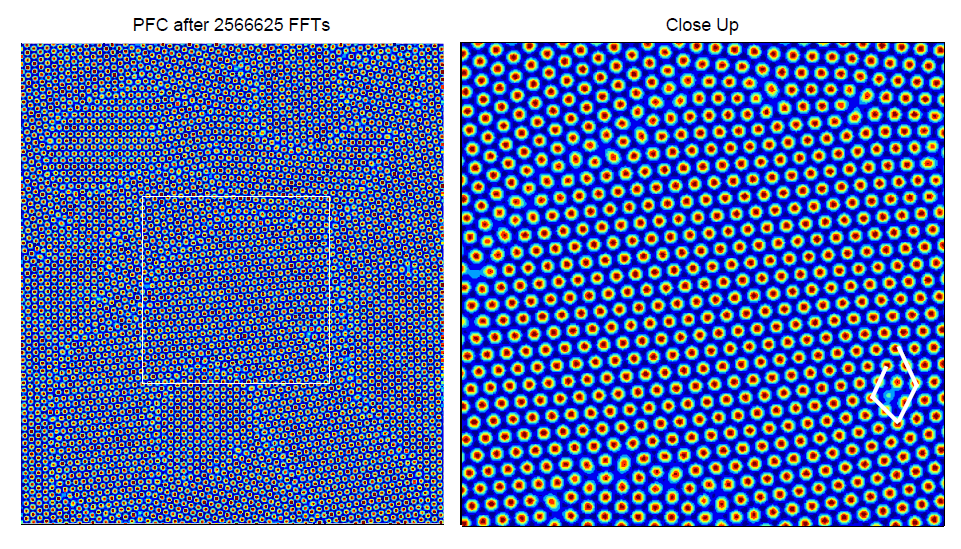

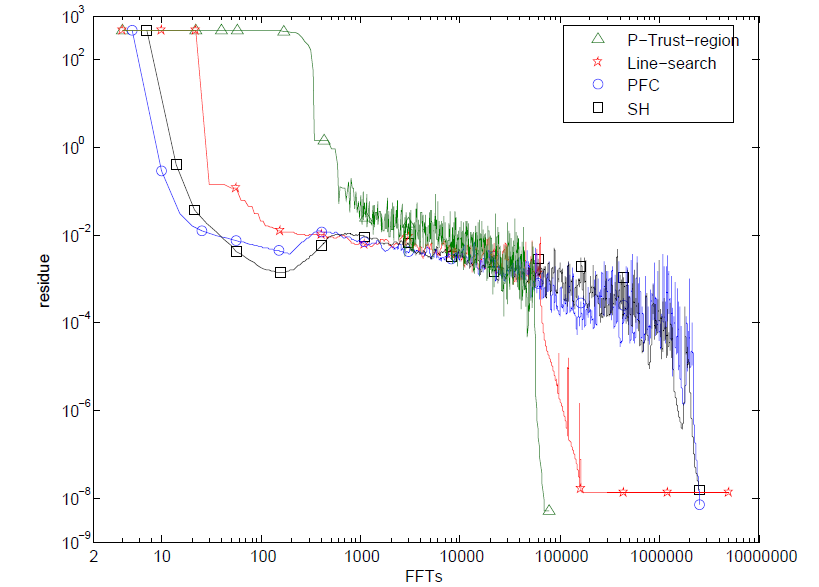
We below show the residue convergence for the four algorithms. In this case our line-search approach appears to be the best
The main new technique we introduce is that of the Łojasiewicz gradient inequality. This allows us toobtain convergence for the gradient flows we use to minimise the PFC functional. For a Hilbert space \( V \) we say that a functional \( \mathcal E \in C^1(V, \mathbb R) \) satisfies the Łojasiewicz gradient inequality near some \( \varphi \in V \), if there exists constants \( \theta \in (0, \frac{1}{2} ], c \ge 0 \) and \( \sigma >0 \) such that for all \( \eta \in V \) with \( \| \eta -\varphi \|_V \le \sigma \)
\( \| \delta \mathcal E(\eta) \|_{V'} \ge c | \mathcal E(\eta) - \mathcal E ( \varphi) |^{1- \theta} \)
see Definition 10.0.3, A. Haraux and M.A. Jendoubi. The Convergence Problem for Dissipative Autonomous
Systems: Classical Methods and Recent Advances. hal-01120022, 2015.
We can now prove a convergence results. Let \(u \) be a trajectory that satisifies the Swift-Hohnberg equation or the PFC equation. Then there exists a \( \varphi \in H^2(\Omega) \) such that \( \delta \mathcal F(\varphi) =0 \) and
\( \displaystyle \lim_{t \to 0}\|u(t)- \varphi \|_{H^2(\Omega)} =0. \)
Moreover, let \( \theta \) be any Łojasiewicz exponent of the PFC functional \( \mathcal F \) at \(\varphi \) . Then we have
\( \| u(t) - \varphi \|_{H} \le \begin{cases} C_e e^{-\beta t} ~~\textrm{ for some } \beta >0 \textrm{ if } \theta = \frac{1}{2} \\ C_t t^ { -\frac{\theta}{1- 2 \theta}} ~~~ \textrm{ if } 0 < \theta < \frac{1}{2} \end{cases} \)
where \( C_e, C_t >0 \) and the \( H \)-norm is the \( L^2 \)-norm for the SH equation and the \( H^{-1} \)-norm for the PFC equation. This result is derived using similar methods to M. Grasselli and H. Wu. chapter Well-posedness and longtime Behaviour for the Modied Phase Field Crystal Equation. Mathematical Models and Methods in Applied Sciences, 24:14, 2014.
During the second term progress is assessed via a PAC meeting.
