Welcome to the webpage of the ERC-funded project “SINGULARITY – Singularities and Compactness in Nonlinear PDEs”, which ran from 2018 to 2024!

The team was primarily based at the Mathematics Institute of the University of WarwickLink opens in a new window.

Our primary funding was from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement 757254), but we also gratefully acknowledge previous funding from the Engineering and Physical Sciences Research Council (EPSRC) and the Lloyds Register Foundation (LRF).

Team:

Filip Rindler (PI)

Paolo Bonicatto (Postdoc 2020-23)
Giacomo Del Nin (Postdoc 2019-2023)
David K. E. Green (Postdoc ATI 2018-2021)
Bogdan Raita (Postdoc 2018-2019)
Adolfo Arroyo-Rabasa (Postdoc 2018-2021)

Dimitrios Andreakis (PhD student 2023-2027)
Kamil Kosiba (PhD student 2015-2019)

Harry Turnbull (Student 2023/24)
Josh Rydell (Student 2023/24)
Natasha Diederen (Student 2022/23)
Jack Lucas (Student 2022/23)
Liam Cox (Student 2021/22)
Balaram Sridhar (Student 2021/22)
Tom Kennedy (Student 2020/21)
Aidan Robertson (Student 2020/21)
Tadashi Matsumoto (Student 2019/20)
Billy Sumners (Student 2018/19)
Robert Johnson (Student 2018/19)

Objectives:

The emergence of singularities, such as oscillations and concentrations, is at the heart of some of the most intriguing problems in the theory of nonlinear PDEs. Rich sources of these phenomena can be found for instance in the equations of mathematical material science and hyperbolic conservation laws.

The SINGULARITY project will investigate singularities through strategies that combine geometric measure theory with harmonic analysis.

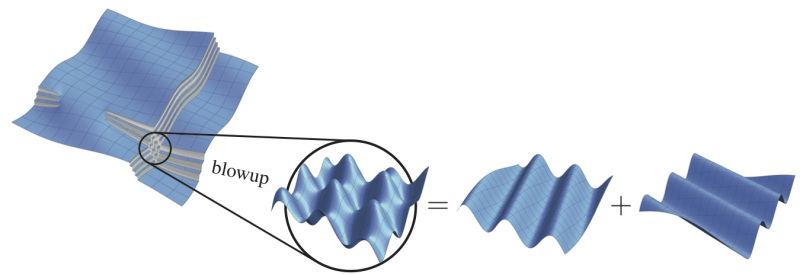
Theme I investigates condensated singularities, i.e. singular parts of (vector) measures solving a PDE and the fine structure theory for PDE-constrained measures.

Theme II is concerned with the development of a compensated compactness theory for sequences of solutions to a PDE, which is capable of dealing with concentrations. The central aim is to study in detail the (non-)compactness properties of such sequences in the presence of asymptotic singularities.

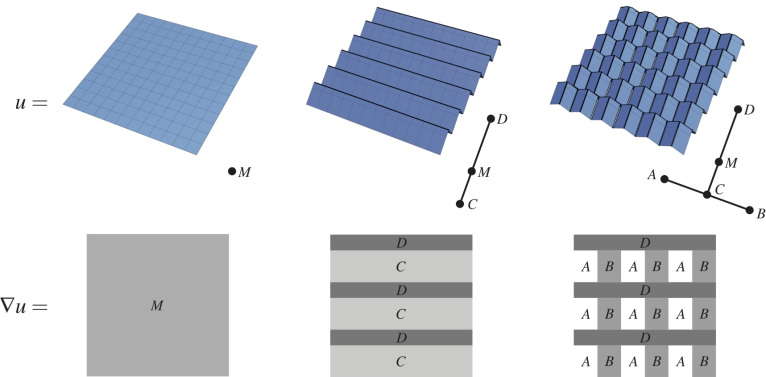
Theme III investigates higher-order microstructure, i.e. nested periodic oscillations in sequences, such as laminates. The main objective is to understand the effective propertiesof such microstructures.

We will also consider applications in Data Science, in particular in the detection & prediction of anomalies in streaming data. This sub-project is part of the Data-Centric Engineering (DCE) programme at the Alan Turing InstituteLink opens in a new windowLink opens in a new window.

A more technical description of recent results can be found in the following survey article: AfreeSurveyLink opens in a new window

Publications:

• Existence and uniqueness for the transport of currents by Lipschitz vector fields (Paolo Bonicatto, Giacomo Del Nin, Filip Rindler), PreprintLink opens in a new windowLink opens in a new window.
• Rigidity of mass-preserving 1-Lipschitz maps from integral current spaces into ℝⁿ (Giacomo Del Nin, Raquel Perales), PreprintLink opens in a new windowLink opens in a new window.
• On the converse of Pansu's Theorem (Guido De Philippis, Andrea Marchese, Andrea Merlo, Andrea Pinamonti, Filip Rindler), PreprintLink opens in a new windowLink opens in a new window.
• Transport of currents and geometric Rademacher-type theorems (Giacomo Del Nin, Paolo Bonicatto, Filip Rindler), PreprintLink opens in a new windowLink opens in a new window.
• Representation of the total variation as a Γ-limit of BMO-type seminorms (Adolfo Arroyo-Rabasa, Paolo Bonicatto, Giacomo Del Nin), PreprintLink opens in a new windowLink opens in a new window.
• Energetic solutions to rate-independent large-strain elasto-plastic evolutions driven by discrete dislocation flow (Filip Rindler), PreprintLink opens in a new windowLink opens in a new window.
• Space-time integral currents of bounded variation (Filip Rindler), PreprintLink opens in a new windowLink opens in a new window.
• Elasto-plastic evolution of single crystals driven by dislocation flow (Thomas Hudson, Filip Rindler), PreprintLink opens in a new windowLink opens in a new window.
• Advection-diffusion equation with rough coefficients: weak solutions and vanishing viscosity (Paolo Bonicatto, Gennaro Ciampa, Gianluca Crippa), PreprintLink opens in a new windowLink opens in a new window.
• A Bourgain-Brezis-Mironescu representation for functions with bounded deformation (Adolfo Arroyo-Rabasa, Paolo Bonicatto), PreprintLink opens in a new windowLink opens in a new window.
• Higher integrability for measures satisfying a PDE constraint (Adolfo Arroyo-Rabasa, Guido De Philippis, Jonas Hirsch, Filip Rindler, Anna Skorobogatova), PreprintLink opens in a new windowLink opens in a new window.

• Endpoint Fourier restriction and unrectifiability (Giacomo Del Nin and Andrea Merlo), PreprintLink opens in a new windowLink opens in a new window.

• Decomposition of integral metric currents (Paolo Bonicatto, Giacomo Del Nin and Enrico Pasqualetto), PreprintLink opens in a new windowLink opens in a new window.

• On the structure of divergence-free measures on R^2 (Paolo Bonicatto and Nikolay A. Gusev), PreprintLink opens in a new windowLink opens in a new window.
• Shape optimization of light structures and the vanishing mass conjecture (Jean-Francois Babadjian, Flaviana Iurlano, Filip Rindler), PreprintLink opens in a new windowLink opens in a new window.
• Continuum limits of discrete isoperimetric problems and Wulff shapes in lattices and quasicrystal tilings (Giacomo Del Nin, Mircea Petrache), PreprintLink opens in a new windowLink opens in a new window.
• Slicing and fine properties of functions with bounded A-variation (Adolfo Arroyo-Rabasa), PreprintLink opens in a new windowLink opens in a new window
• Debye screening for the stationary Vlasov-Poisson equation in interaction with a point charge (Adolfo Arroyo-Rabasa, Raphael Winter), PreprintLink opens in a new windowLink opens in a new window
• Probabilistic solution of chaotic dynamical system inverse problems using Bayesian Artificial Neural Networks(David K. E. Green, Filip Rindler), PreprintLink opens in a new windowLink opens in a new window
• Rectifiability of the jump set of locally integrable functions (Giacomo Del Nin), PreprintLink opens in a new windowLink opens in a new window
• Geometric criteria for C^{1,α} rectifiability (Giacomo Del Nin, Kennedy Obinna Idu), PreprintLink opens in a new windowLink opens in a new window
• On the fine properties of elliptic operators (Adolfo Arroyo Rabasa, Anna Skorobogatova), PreprintLink opens in a new windowLink opens in a new window
• Fine properties of functions of bounded deformation – an approach via linear PDEs (Guido De Philippis, Filip Rindler), PreprintLink opens in a new windowLink opens in a new window
• Quasiconvexity, null Lagrangians, and Hardy space integrability under constant rank constraints (A. Guerra, B. Raita), PreprintLink opens in a new windowLink opens in a new window
• Characterization of generalized Young measures generated by A-free measures (A. Arroyo-Rabasa), PreprintLink opens in a new windowLink opens in a new window
• Two-speed solutions to non-convex rate-independent systems (F. Rindler, S. Schwarzacher, J. J. L. Velazquez), PreprintLink opens in a new windowLink opens in a new window
• Concentration versus oscillation effects in brittle damage (J.-F. Babadjian, F. Iurlano, F. Rindler), PreprintLink opens in a new windowLink opens in a new window
• A Note on Estimates for Elliptic Systems with L1 Data (B. Raita, D. Spector), PreprintLink opens in a new windowLink opens in a new window
• Model inference for ordinary differential equations by parametric polynomial kernel regression (D. K. E. Green, F. Rindler), PreprintLink opens in a new windowLink opens in a new window
• On limiting trace inequalities for vectorial differential operators (F. Gmeineder, B. Raita, J. Van Schaftingen), PreprintLink opens in a new windowLink opens in a new window.
• On the relaxation of integral functionals depending on the symmetrized gradient (K. Kosiba, F. Rindler), PreprintLink opens in a new windowLink opens in a new window
• Continuity and canceling operators of order n on ℝ^n (B. Raita, A. Skorobogatova), PreprintLink opens in a new windowLink opens in a new window.
• Generalized multi-scale Young measures (A. Arroyo-Rabasa, J. Diermeier), PreprintLink opens in a new windowLink opens in a new window
• An elementary approach to the dimension of measures satisfying a first-order linear PDE constraint (A. Arroyo-Rabasa), PreprintLink opens in a new windowLink opens in a new window.
• L1-estimates for constant rank operators (B. Raita), PreprintLink opens in a new windowLink opens in a new window.
• Dimensional estimates and rectifiability for measures satisfying linear PDE constraints (A. Arroyo-Rabasa, G. De Philippis, J. Hirsch, F. Rindler), PreprintLink opens in a new windowLink opens in a new window.
• Relaxation for partially coercive integral functionals with linear growth (F. Rindler, G. Shaw), PreprintLink opens in a new windowLink opens in a new window.
• On the two-state problem for general differential operators (G. De Philippis, L. Palmieri, F. Rindler), Online versionLink opens in a new windowLink opens in a new window, PreprintLink opens in a new windowLink opens in a new window.
• On the structure of measures constrained by linear PDEs (G. De Philippis, F. Rindler), PreprintLink opens in a new windowLink opens in a new window.
• Liftings, Young measures, and lower semicontinuity (F. Rindler, G. Shaw), Online version (Open access).Link opens in a new window