Seminars are held on Mondays at 17:00 in B3.02
Organisers: Adam Thomas and Gareth Tracey
(To see the abstract and title of a talk in the past, click on the speakers name to expand it)
Term 2:
15th January: Jonathan Gruber (York)
Title: Stabilization of cohomology for Frobenius kernels
Abstract: Let G be a simple algebraic group over an algebraically closed field of positive characteristic. The Frobenius kernels of G are an ascending chain of finite normal subgroup schemes of G, which arise by taking the scheme theoretic kernels of the powers of a Frobenius morphism on G. Many aspects of the representation theory of G are controlled by the collection of all Frobenius kernels; for instance, the G-fixed points in a finite-dimensional G-module coincide with the fixed points under some sufficiently large Frobenius kernel. In this talk, we will discuss a derived analogue of this statement: For any sufficiently large Frobenius kernel, the G-cohomology of a finite-dimensional G-module can be recovered from the cohomology over the Frobenius kernel via the restriction map in cohomology. This is joint work with Daniel K. Nakano.
22nd January: David Stewart (Manchester)
Title: You need 27 tickets to guarantee a win on the UK National Lottery (Jt with David Cushing)
Abstract: The authors came across the problem of finding minimal lottery design numbers j=L(n,k,p,t); that is, a set B1, …, Bj subsets of {1,..,n} each of size k, such that for any subset D of {1,..,n} of size p, one finds an intersection D\cap B_i with at least t elements. In the context of a lottery, n represents the. number of balls, k the number of choices of balls on a ticket, p the size of a draw. For the UK national lottery, n=59, k=p=6 and one gets a (rather meagre) prize as long as t is at least 2. Using the constraint solving library in Prolog, we calculated j for k=p=6, t=2 and n all the way up to 70. For example L(59,6,6,2)=27. This is the second paper where we have aimed to show the value of Prolog and constraint programming in pure mathematics. I'll give an overview of constraint programming, logic programming in Prolog, and describe how we used these tools to solve the problem described in the title.
29th January: Hong Yi Huang (Bristol)
Title: Bases for permutation groups
Abstract: Let G < Sym(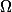 ) be a permutation group on a finite set
) be a permutation group on a finite set 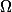 . A base for G is a subset of Omega with trivial pointwise stabiliser, and the base size of G, denoted b(G), is the minimal size of a base for G. This classical concept has been studied since the early years of permutation group theory in the nineteenth century, finding a wide range of applications. Recall that G is called primitive if it is transitive and its point stabiliser is a maximal subgroup. Primitive groups can be viewed as the basic building blocks of all finite permutation groups, and much work has been done in recent years in bounding or determining the base sizes of primitive groups. In this talk, I will report on recent progress of this study. In particular, I will give the first family of primitive groups arising in the O'Nan-Scott theorem for which the exact base size has been computed in all cases.
. A base for G is a subset of Omega with trivial pointwise stabiliser, and the base size of G, denoted b(G), is the minimal size of a base for G. This classical concept has been studied since the early years of permutation group theory in the nineteenth century, finding a wide range of applications. Recall that G is called primitive if it is transitive and its point stabiliser is a maximal subgroup. Primitive groups can be viewed as the basic building blocks of all finite permutation groups, and much work has been done in recent years in bounding or determining the base sizes of primitive groups. In this talk, I will report on recent progress of this study. In particular, I will give the first family of primitive groups arising in the O'Nan-Scott theorem for which the exact base size has been computed in all cases.
5th February: Beth Romano (Kings College London)
Title: Constructing graded Lie algebras
Abstract: I'll talk about a construction that starts with a Heisenberg group of a certain kind and produces a graded Lie algebra. While purely algebraic, this construction is motivated by questions in number theory about rational points on families of curves, a setting where graded Lie algebras have proven to give valuable information. In addition to the number-theoretic applications, the construction has some nice applications to Lie theory, giving a way to lift certain Weyl group elements. I won't assume any background knowledge about graded Lie algebras or algebraic curves, and I'll give examples throughout the talk.
12th February: Rudradip Biswas (Warwick)
Title: Algebraic conditions for discrete groups to admit finite dimensional models for their classifying space of proper actions
Abstract: Amongst people caring about cohomology questions for infinite groups, having a neat checkable algebraic property that, when imposed on a group G, implies the existence of a finite dimensional model for \underline{E}G has been a stimulating question for more than two decades. In this talk, I will try to highlight my contributions to this question. I will make sure to provide all the necessary definitions. My hope is the talk will be accessible to anyone with a basic knowledge of group cohomology. A part of the material is already in published form - "Injective generation of derived categories and other applications of cohomological invariants of infinite groups." Comm. Algebra 50 (2022), no. 10, 4460-4480.
19th February: Josh Maglione (Galway)
Title: Automorphisms of groups from elliptic curves
Abstract: We describe a group scheme coming from an elliptic curve over a field K. We characterize when two (abstract) groups arising in this way are isomorphic, and we use this to describe the automorphism group of such groups. This generalizes work of du Sautoy--Vaughan-Lee and Stanojkovski--Voll. This is joint with Mima Stanojkovski.
26th February: Martina Balagovic (Newcastle)
Title: Quantum symmetric pairs coideal subalgebras
Abstract: I will explain the motivation, history, and some recent progress in the theory of quantum symmetric pairs and their representations. Quantum symmetric pairs are certain defomations of universal enveloping algebras of Lie algebras, different to the standard Drinfeld Jimbo quantum groups but realised as their coideals. Just like the construction of the universal R-matrix for quantum groups produces solutions of the Yang-Baxter equation and gives an action of the braid group of type A on the category of their finite dimensional representations, quantum symmetric pairs allow an analogous construction of a universal K-matrix, producing solutions of the reflection equation and giving an action of the braid group of type B. I will also explain some recent constructions in their representation theory, which is work in progress. All this is joint work with Stefan Kolb.
4th March: Paul Levy (Lancaster)
Title: Special pieces in exceptional Lie algebras
Abstract: In connection with the Springer correspondence, Lusztig defined an important subset of the nilpotent orbits in a simple Lie algebra, called the special orbits. To each special orbit is associated an open subset of its closure, called a special piece; the special pieces partition the nilpotent cone. A long-standing conjecture of Lusztig, open in exceptional types, is that each special piece is the quotient of a smooth variety by a certain finite group H. In this talk I will outline a proof of the conjecture. The first step is the establishment of a "local version" of the conjecture, which holds in a suitable transverse slice. In each case, the transverse slice is isomorphic to the quotient of a vector space by H. The local version allows us to establish smoothness of a certain H-cover of the special piece, therefore establishing the conjecture. Along the way, we observe various interesting symplectic quotient singularities appearing as transverse slices between nilpotent orbits in exceptional Lie algebras. This is joint work with Fu, Juteau and Sommers.
11th March: Eileen Pan (Warwick)
Title: Some coset actions in G_2(q)
Abstract: The coset actions of almost simple groups have sparked much interest and a lot has been done by various authors, but there remains much to explore. In this talk we consider \(G \cong G_2(q)\) for some prime power \(q\) and let \(H \le G\) be a maximal-rank maximal subgroup of \(G\). We describe the double cosets \(\{HgH: g \in G\}\) and the corresponding intersections \(H \cap H^g\). This in turn gives us the suborbit representatives and subdegrees of the coset action of \(G\) on \(H \backslash G \). Along the way, we give a brief overview of some known results in algebraic and finite groups of exceptional Lie type and explain how they are used in approaching this problem.
Term 1:
9th October: Christian Ikenmeyer (Warwick)
Title: All Kronecker coefficients are reduced Kronecker coefficients
Abstract: We settle the question of where exactly the reduced Kronecker coefficients lie on the spectrum between the Littlewood-Richardson and Kronecker coefficients by showing that every Kronecker coefficient of the symmetric group is equal to a reduced Kronecker coefficient by an explicit construction. This implies the equivalence of a question by Stanley from 2000 and a question by Kirillov from 2004 about combinatorial interpretations of these two families of coefficients. This is joint work with Greta Panova, arXiv:2305.03003.
16th October: Stacey Law (Birmingham)
Title: Sylow branching coefficients for symmetric groups
Abstract: One of the key questions in the representation theory of finite groups is to understand the relationship between the characters of a finite group G and its local subgroups. Sylow branching coefficients describe the restriction of irreducible characters of G to a Sylow subgroup P of G, and have been recently shown to characterise structural properties such as the normality of P in G. In this talk, we will discuss and present some new results on Sylow branching coefficients for symmetric groups.
23rd October: Veronica Kelsey (Manchester)
Title: Nice and Nasty Numerical Invariants
Abstract: For a permutation group G we can define the maximal irredundant base size and the relational complexity, denoted I(G) and RC(G) respectively. Roughly speaking the maximal irredundant base size is the size of the “worst” base for G, and relational complexity is a measure of when a local property extends to a global one.
We begin by defining these numerical invariants and then cover some examples which illustrate the “nice” behaviour of I(G) and the “nasty” behaviour of RC(G). We’ll then skim through the proof of the relational complexity of a family of groups.
30th October: Lucia Morotti (York)
Title: Self-extensions for irreducible representations of symmetric groups
Abstract: It has been conjectured that irreducible representations of symmetric groups have no non-trivial self-extensions in characteristic different from 2, that is that the only modules V with 2 composition factors isomorphic to D for some irreducible module D and no other composition factor are those of the form D + D. This conjecture has been proved for some classes of modules by Kleshchev-Sheth and Kleshchev-Nakano. I will present joint results with Harry Geranios and Sasha Kleshchev and current work with Harry Geranios considering reduction results and generalisations of the above mentioned papers.
6th November: Martin van Beek (Manchester)
Title: Exotic Fusion Systems Related to Sporadic Simple Groups
Abstract: Fusion systems offer a way examine and express properties of the p-conjugacy of elements in finite groups. However, not every fusion system may be constructed from a finite group in an appropriate way. This gives rise to exotic fusion systems. An important research direction involves the study of the behaviour of exotic fusion systems (in particular at odd primes).
In this talk, we describe several exotic fusion systems related to the sporadic simple groups at odd primes. More generally, we classify saturated fusion systems supported on Sylow 3-subgroups of the Conway group Co1 and the Thompson group F3, and a Sylow 5-subgroup of the Monster M, as well as a particular maximal subgroup of the latter two p-groups. This work is supported by computations in MAGMA.
13th November: Peiran Wu (St Andrews)
Title: Irredundant bases for the symmetric and alternating groups
Abstract: An irredundant base of a group G acting faithfully on a finite set Γ is a sequence of points in Γ that produces a strictly descending chain of pointwise stabiliser subgroups in G, terminating at the trivial subgroup. I will give an overview of known results about the irredundant base size, before focusing on the case where G is the symmetric or alternating group of degree n with a non-standard primitive action. It was proved in 2011 that an irredundant base of size 2 exists for such an action in all but finitely many cases. I will speak about the recent work by me and my supervisor, where we have shown that the maximum size of an irredundant base for the action is O(√n) and in most cases O((log n)^2). These upper bounds are also best possible in their respective cases, and I will present some interesting examples constructed to prove their optimality.
20th November: Matthew Chaffe (Birmingham)
Title: Composition multiplicities of Verma modules for truncated current Lie algebras
Abstract: The problem of computing the composition multiplicities of Verma modules for a semisimple Lie algebra was famously solved by the proof of the Kazhdan-Lusztig conjecture, which gives the multiplicities in terms of certain polynomials known as the Kazhdan-Lusztig polynomials. In this talk, I will discuss this problem for a related class of Lie algebras, known as truncated current Lie algebras. I will also discuss the BGG category O of modules for a semisimple Lie algebra and an analogue of this category for truncated current Lie algebras.
27th November: Iulian Simion (Babeș-Bolyai University)
Title: Growth in simple algebraic groups via unipotent elements
Abstract: Let G be a simple algebraic group over an algebraically closed
field and let A be a generating subset of G. We are interested in the
smallest integer m such that G=A^m. We discuss some aspects of this
problem with emphasis on unipotent elements. In particular we discuss
the case where A is a unipotent conjugacy class and recent contributions
to bounds on covering numbers.
4th December: Tim Burness (Bristol)
