Organisers: Ferran Brosa Planella and Thomasina Ball

The Applied Maths Seminars are held on Fridays 12:00-13.00. This year the seminar will be hybrid (at least for Term 1): you can choose to attend in person in room B3.02 or on MS Teams. The team for the seminar is the same as last year, but if you are not a member, you can send a membership request via MS Teams or email the organisers.

Please contact Ferran Brosa Planella or Thomasina Ball if you have any speaker suggestions for future terms.

Seminar Etiquette: Here is a set of basic rules for the seminar.

• Please keep your microphone muted throughout the talk. If you want to ask a question, please raise your hand and the seminar organiser will (a) ask you to unmute if you are attending remotely or (b) get the speaker's attention and invite you to ask your question if you are in the room.
• If you are in the room with us, the room microphones capture anything you say very easily, and this is worth keeping in mind ☺️.
• You can choose to keep your camera on or not. Colleagues in the room will be able to see the online audience.
• Please let us know if you would like to meet and/or have lunch with any of the speakers who are coming to visit us so that I can make sure you have a place in the room.

Term 3

Term 2

Term 1

Abstracts

Term 3

Week 2.

(a) Joseph Webber (Warwick) - A linear-elastic-nonlinear-swelling model for hydrogels

Hydrogels are an important example of poroelastic materials, formed from hydrophilic polymer chains surrounded by adsorbed water molecules. Key to many of their uses is the fact that they can swell to hundreds of times their initial size upon imbibition of water, but at any swelling state they behave as solid, soft, elastic media. Modelling such gels can be challenging: large-strain elasticity arising from swelling and drying must be incorporated alongside the interaction between water and polymer molecules and the transport of water through the pore spaces. This has, in the past, led to many complicated nonlinear approaches based on deriving a free energy density from a bottom-up understanding of the molecular-scale dynamics. In this talk, I will summarise a new model for the dynamics of hydrogels that treats them as instantaneously incompressible linear-elastic materials, whilst allowing for nonlinearities in the isotropic strains corresponding to swelling. This approach is not only analytically tractable, but also able to describe the gel using only three (macroscopic) swelling-state-dependent material parameters. I will discuss the new predictions that such a model can make and show how the aforementioned material parameters for any gel could be easily determined experimentally.

(b) Julio Hurtado (Warwick) - Continual Learning in Deep Learning and how this impact my research in CAMaCS

Deep Learning models rely on a fixed and limited dataset to learn. This strategy works fine as long as the test data remains similar to the train distribution. However, when the test set changes, we must retrain the model by adjusting its weight to learn the latest distribution. One naive solution is to train the model with the new distribution, which modifies the weight of the model but overwrites previous knowledge and forgets previous distributions. Continual Learning is a technique that aims to train a model continuously over a stream of changing datasets, aiding with the mitigation of forgetting previous tasks. In this talk, I will discuss how we can indirectly tackle the forgetting of previous data by addressing the issue of generalisation, and how this is guiding my research in CAMaCS.

Week 3. Katarzyna Macieszczak (Warwick) - Metastability in Open Quantum Systems

Week 4. Yuyang Zhou (Edinburgh Napier) - Fully Probabilistic Control Algorithm Design for a class of Complex Stochastic Systems

Complex dynamical systems have garnered significant interest in the realms of control and engineering, as they offer a cohesive and natural framework for the mathematical modeling of diverse real-world systems, such as communication networks, power grids, and chemical processes. The inherent characteristics of these systems, such as high dimensionality, intricate structures, complex models with multiple modes of switching, and substantial uncertainties, pose notable challenges for system analysis, estimation, and particularly for control.

This talk will introduce a novel decentralised probabilistic control framework designed for complex stochastic systems. It will offer a fresh research outlook dedicated to refining the control of such systems. In this talk, we will delineate the core principles and applications of the framework, showcasing its contribution to the development of innovative control strategies for complex stochastic systems.

Week 5. Valeria Giunta (Swansea) - Bifurcations, pattern formation and multi-stability in non-local models of interacting species

Understanding the mechanisms behind the spatial distribution, self-organisation and aggregation of organisms is a central issue in both ecology and cell biology. Since self-organisation at the population level is the cumulative effect of behaviours at the individual level, it requires a mathematical approach to be elucidated.

In nature, every individual, be it a cell or an animal, inspects its territory before moving. The process of acquiring information from the environment is typically non-local, i.e. individuals have the ability to inspect a portion of their territory. In recent years, a growing body of empirical research has shown that non-locality is a key aspect of movement processes, while mathematical models incorporating non-local interactions have received increasing attention for their ability to accurately describe how interactions between individuals and their environment can affect their movement, reproduction rate and well-being. In this talk, I will present a study of a class of advection-diffusion equations that model population movements generated by non-local species interactions. Using a combination of analytical and numerical tools, I will show that these models support a wide variety of spatio-temporal patterns that are able to reproduce segregation, aggregation and time-periodic behaviours commonly observed in real systems. I will also show the existence of parameter regions where multiple stable solutions coexist and hysteresis phenomena.

Overall, I will describe various methods for analysing bifurcations and pattern formation properties of these models, which represent an essential mathematical tool for addressing fundamental questions about the endless aggregation phenomena observed in nature.

Week 6. Giulia Celora (UCL) - Self-organized patterning in complex fluids

Understanding how multicomponent systems self-organise to control their emergent dynamics across spatial and temporal scales is a fundamental problem with important applications in many areas; from the design of soft materials to the study of developmental biology. In this talk, I will discuss how we can use mathematical modelling to understand the role of microscale physical interactions in the self-organisation of complex fluids. I will illustrate this by presenting two examples. Firstly, I will discuss self-organization in stimuli-responsive polyelectrolyte gels surrounded by an ionic solution; secondly, I will discuss self-organization during collective migration of multicellular communities. Our results reveal hidden connections between these two initially disconnected applications hinting at the existence of general principles controlling self-organisation of both inanimate and living matter.

Week 7. Roberto Alamino (Aston) - Machine Learning in Statistical Physics & Condensed Matter - Physical Information and Explainability

The talk will provide an overview of some key applications of machine learning (ML) to problems involving condensed matter and statistical physics taking a closer look into two main issues: (i) the role played by physical information in the design of the ML models and (ii) the explainability of the trained parameters and the possibility of extracting meaningful physics from them.

Week 8. Sara Jabbari (Birmingham) - Mathematical tools to aid with the development of novel antimicrobials

The ability of bacteria to become resistant to previously successful antibiotic treatments is an urgent and increasing worldwide problem. Solutions can be sought via a number of methods including, for example, identifying novel antibiotics, re-engineering existing antibiotics or developing alternative treatment methods. The nonlinear interactions involved in infection and treatment render it difficult to predict the success of any of these methods without the use of computational tools in addition to more traditional experimental work. We use mathematical modelling to aid in the development of anti-virulence treatments which, unlike conventional antibiotics that directly target a bacterium's survival, may instead attenuate bacteria and prevent them from being able to cause infection or evade antibiotics. Many of these approaches, however, are only partially successful when tested in infection models. Our group are studying a variety of potential targets, including preventing bacteria from binding to host cells, inhibiting the formation of persister cells (these can tolerate the presence of antibiotics) and blocking efflux pump action (a key mechanism of antimicrobial resistance). I will present results that illustrate how mathematical modelling can suggest ways in which to improve the efficacy of these approaches.

Week 9. Lukas Eigentler (Warwick) - Modelling dryland vegetation patterns

**Disclaimer: I gave the same talk at the SBIDER seminar in January.** Vegetation patterns are a ubiquitous feature of semi-arid regions and are a prime example of a self-organisation principle in ecology. In this talk, I present a broad overview of how I have used mathematical modelling and analysis to develop new insights into vegetation pattern dynamics, for example on how different plant species can coexist despite competition for a single limiting resource, and a possible resolution for contradicting field data on the long-term migration dynamics of vegetation patterns.

Week 10

(a) Lucas Araujo Bonomo (Warwick) - On the modelling of acoustic liners with grazing flow

Acoustic liners are passive devices installed on the interior walls of modern aircraft turbofan nacelles to mitigate fan noise. These devices are typically characterized by their acoustic impedance, which can be utilized in numerical and analytical models of turbofan engines to predict noise attenuation. The presence of a sheared grazing flow over an acoustic absorptive surface alters the acoustic attenuation provided by the surface, necessitating adjustments in the boundary conditions to account for this phenomenon. In this talk, I will introduce the current models available in the literature and discuss the ongoing debate regarding their application.

(b) Duygu Sap (Warwick) - Structure Preserving Finite Element Methods

In this talk, I will describe the construction of structure-preserving finite element methods for solving partial differential equations that govern incompressible fluid flow and some solid mechanics problems, such as linear elasticity. These methods utilize algebraic complexes, precisely, the de Rham and BGG complexes, to ensure the preservation of topological properties.

Term 2

Week 1. Masoud Jabbari (Leeds) - Physics-based modelling of battery electrode drying

The drying process and its influencing parameters during electrode manufacturing has a
crucial impact on the structural integrity, and thence, the performance of lithium-ion battery
cells. A physics-based model is developed on a Representative Elementary Volume (REV)
scale where non-isothermal multi-phase compositional porous-media flow and single-phase
compositional laminar free-flow are coupled [1]. The developed model is used to analyse the
influence of ventilation speed magnitude, v_max, the equivalent diameter of particles of the
porous medium, d_p, the porosity of the porous medium, ϕ, the initial temperature in the
free-flow region, T^ff, and the initial temperature in the porous-medium region, T^pm, on the
characteristic drying curves [2]. The effects of varying each of the parameters are shown
with particular attention to the maximal drying rate as well as the final time for the drying
process, which are both key factors in electrode drying [3].

[1] Jabbari, M., et al. "Drying of a tape-cast layer: numerical modelling of the evaporation process in a graded/layered material." International Journal of Heat and Mass Transfer 103 (2016): 1144-1154.

[2] Jabbari, M., et al. "Drying of a tape-cast layer: Numerical investigation of influencing parameters." International Journal of Heat and Mass Transfer 108 (2017): 2229-2238.

[3] Jabbari, Masoud, et al. "Ceramic Manufacturing for Green Energy Applications." Applied Complex Flow: Applications of Complex Flows and CFD (2023): 149-168.

Week 3. Madeleine Moore (Hull) - An asymptotic solution for evaporation of arbitrary-shaped droplets

Diffusion-limited evaporation of liquid droplets has received significant research interest due to its fundamental significance in a variety of industrial and engineering applications such as inkjet printing, microscale and colloidal patterning, DNA microarray technologies and the manufacture of Q/OLEDs. However, beyond circular and elliptical droplets, there are very few existing analytical solutions, despite a number of these applications exhibiting droplets of a more complex geometry. Here, we address this deficiency by deriving asymptotic results for the evaporative flux of a weakly non-circular droplet. We demonstrate how the framework may be extended to polygonal geometries and droplet arrays, with an eye to industrial applications.

Week 4. Matt Butler (UCL) - Swelling hydrogels by heating and cooling

Hydrogels are soft hydrophilic polymeric materials that absorb water, causing significant swelling. Their biocompatibility and compliance have found many applications, including in contact lenses, wound healing patches, targeted drug delivery, and water retention in soils. Responsive hydrogels are a class of hydrogel whose degree of swelling depend on a stimulus (e.g. pH, light or electromagnetism). This control of size gives opportunity to design shape change, since structures can be designed with differential swelling/shrinking that causes programmed deformation. In this talk, I will present recent work on poro-elastic modelling of the swelling behaviour of thermo-responsive hydrogels, and discuss how these hydrogels can be used to design components for microsystems.

Week 5. Karen Estefanía Loayza Romero (Imperial) - Compliance minimisation problems under a fully discrete shape optimisation framework

Compliance minimisation problems aim to find as stiff structures as possible for prescribed volumes, which can be used for designing bridges, offshore structures, turbomachinery, or biomedical devices. Usually, they are treated as topology optimisation problems, which, unfortunately, are highly ill-posed and often exhibit solutions with micro-structures which are difficult to treat numerically and more importantly to manufacture.

One way to guarantee the existence of solutions for this problem is to fix the topology (the number of holes) of the structure, which transforms the problem into a shape optimisation problem. However, even by treating them as shape optimization problems many drawbacks remain, for example, the discrepancies in the existence of solutions between the continuous and discretized problems, and the increasing mesh degeneracy along the optimisation process.

In this talk, we focus on developing a framework which allows us to solve fully discrete shape optimisation problems based on the assumption that discrete shapes are triangular meshes, and they form a smooth manifold. This manifold will be endowed with a particular complete Riemannian metric which takes care of the mesh degeneracy and helps us to render a regularization to guarantee the existence of solutions.

Week 6. Anna Kalogirou (Nottingham) - The role of soluble surfactants on the stability of two-layer flow in a channel

This work investigates the impact of surfactant on the interfacial stability of a two-layer shear flow in a channel. The surfactant molecules can get adsorbed at the interface or form micellar aggregates when their concentration is beyond a critical value. A mathematical model is formulated that describes the hydrodynamics and transport of surfactant. The effect of surfactants on the stability of the flow is investigated via a linear stability analysis, and the identified instabilities are followed into the nonlinear regime by carrying out numerical computations of a lubrication-type system. The range of validity of the asymptotic model is estimated by carrying out comparisons with direct numerical simulations (DNS) of the full system of governing equations.

Week 7. Eric Rogers (Southampton) - Optimization-based Iterative Learning Control with Applications in Physics, Engineering, and Healthcare

Many physical systems complete the same finite-duration task over and over again. One example in robotic applications is the `pick and place’ task, where the mission is to move a sequence of payloads from a fixed location and place them in synchronization on a moving conveyor. The series of operations is as follows: i) collect the payload from the specified location, ii) transfer it over a finite duration, iii) place it on the moving conveyor, iv) return to the starting location, and repeat this sequence for as many payloads as required or until a stop is required for maintenance or other reasons.

Iterative learning control emerged in the mid-1980s for application to examples such as the one just described, and since then has been a very active research and applications area. This seminar will first describe the development of an optimization-based design in a Hilbert space setting and then demonstrate its application, with supporting experimental results, to free-electron lasers, rack feeders, and robotic-assisted stroke rehabilitation. Some currently open research problems will also be briefly discussed.

Week 8. Fiona Macfarlane (St Andrews) - Discrete and continuum methods to describe cancer invasion processes

The ability of biological cell populations to correlate their movement and proliferation processes can result in collective migration and evolving spatio-temporal patterns at the cellular population level. These collective mechanisms play an important role in the formation and growth of solid tumours. We have formulated agent-based models of cancer invasion wherein the infiltrating cancer cells may occupy a spectrum of states in phenotype space, for example ranging from `fully mesenchymal' to `fully epithelial'. The more mesenchymal cells are those that display more migratory phenotypes, where we examine directed cell movement such as haptotaxis or pressure-dependent movement. However, as a trade-off, they have lower proliferative capacity than the more epithelial cells. We have then formally derived the corresponding continuum models, which takes the form of partial integro-differential equations for the local cell population density function. Despite the intricacy of these models, for certain parameter regimes it is possible to carry out detailed travelling wave analyses and obtain invading fronts with spatial structuring of phenotypes. As such, the models recapitulate similar observations into the structures of invading waves into leader-type and follower-type cells, witnessed in an increasing number of experimental studies over recent years.

Week 9.

(a) Peter Lewin-Jones (Warwick) - Impacts of Liquid Drops: When Do Gas Microfilms Prevent Merging?

Collisions and impacts of drops are critical to numerous processes, including raindrop formation, inkjet printing, food manufacturing and spray cooling. For drop-drop collisions, increasing the relative speed leads to multiple transitions: from merging to bouncing and then back to merging - transitions which were recently discovered to be sensitive to the drops' radii as well as the ambient gas pressure. The outcome of a drop impacting a liquid bath is even more complex: for a fixed speed, the result can go from merging to bouncing to merging and back to bouncing with increasing bath depth.

To provide new insight into the physical mechanisms involved and as an important predictive tool, we have developed a novel, open-source computational model for both drop-drop and drop-bath events, using the finite element package oomph-lib. This uses a lubrication framework for the gas film and incorporates fully, for the first time, the crucial micro- and nano-scale influences of gas kinetic effects and disjoining pressure.

Our simulations show strong agreement with experiments for the transitions between merging and bouncing, but can also go beyond these regimes to make new experimentally-verifiable predictions. We will show how our model enables us to explore the parameter space and discover the regimes of contact (that are inaccessible to experiments). Finally, we will overview potential extensions to the computational model, including impacts in Leidenfrost conditions and post-contact dynamics.

(b) Iain Souttar (Warwick) - From averaging methods to biophyisical modelling, and nowhere in between

A popular way of reducing the complexity of multiscale systems is through the method of averaging. Historically, averaging is known to provide a good approximation to the fully coupled system (here we will consider a system of SDEs) over finite time horizons. After having introduced averaging, results showing that the distance between the averaged system and the fully coupled system can be bounded uniformly in time will be given, along with potential applications in Statistics and Mathematical Biology.

I have recently started as an InRA here at Warwick in CAMaCS (Centre for Applications of Mathematical & Computing Sciences) and so in the second half of the talk I will describe one of the current projects, modelling the bonds between tubulins which make up microtubules. Microtubules are an important component of the cytoskeleton and exhibit complex growth/degrowth behaviour. We will study the lattice shape of these structures and discuss the effect of kinesin-microtubule interaction mechanisms.

Week 10. Jay Warnett (Warwick) - X-ray Computed Tomography – Practical Iterative Image Reconstruction

X-ray Computed Tomography (XCT) has transcended its medical origins, becoming indispensable in manufacturing due to its ability to non-destructively observe internal structures and flaws. Its application at WMG is even more diverse including conservation in museums and police forensic investigations. However, its use is primarily restricted to high value items given the cost of an XCT system and scan duration, ranging from 30 minutes to several hours. To exploit it within in-line manufacturing processes this needs to become an order of magnitude faster to enable a reasonable throughput.

An XCT scan involves positioning the object between an X-ray source and detector, capturing projections through 360 degrees. Reconstruction algorithms then convert these projections into CT slices. The industry-standard analytical method Feldkamp-Davis-Kress (FDK) is fast and broadly produces a good result, but requires high-quality projections and a substantial number of them - around 3000 for a 2000 pixel width detector. Speeding up acquisition means acquiring limited data - either noisier lower-quality projections, fewer projections or a combination of both, leading to challenges for FDK. Iterative methods are significantly better at working with limited data - at least in theory. With noise in the projections, instead of converging to CT slices that best represent the object it will converge to a naïve solution containing all the noise components. We can introduce regularisers to encourage the iterations of your chosen method towards more reasonable solutions but there are practical limitations on problems of this size.

We want to limit the acquired data as much as possible, implement iterative reconstruction but maintain an accurate representation of the object in the CT slice. Perfecting this process is therefore a necessity as the potential ramifications of missing a defect through altering this process range from financial losses to safety hazards. In this talk we explore XCT at WMG, discuss reconstruction theory, acknowledge practical constraints, and discuss our integration of iterative methods to enhance imaging throughput.

Term 1

Week 1. Francesca Arrigo (Strathclyde) - f(A)bulous networks: an overview of matrix functions in network science

Though seemingly they belong to two different worlds, matrix functions and network science have some degree of overlap thanks to a very simple fact; powers of the adjacency matrix count traversals in the underlying network. This concept in turn allows for the definition of centrality measures in terms of entries (or sums thereof) of functions of the adjacency matrix.

In this talk, after reviewing basic definitions, we will give an overview of popular walk-based centrality measures in networks, emphasizing the role of matrix functions and of expressions of the form f(A)b and c^T f (A)b. We will further discuss nonbacktracking walk-based centralities and describe challenges and open problems.

Week 2. Lyndon Koens (Hull) - Modelling Microscopic Swimmers

Microscopic swimmers exist in diverse and complex environments and use many different forms of propulsion and feeding. Biological microswimmers play key roles in many ecosystems, while artificial microswimmers could be used for targeted drug delivery, or the development of new keyhole surgeries. Modelling and understanding the behaviour of such swimmers is however a non-trivial task. In this talk I will provide a brief overview of the swimming problem before talking about some of my recent work on modelling the behaviour of microscopic swimmers.

Week 3. Oana Lang (Imperial) - Eulerian calibration for stochastic models

Stochastic partial differential equations are widely used to model the evolution of uncertain dynamical systems in geophysical fluid dynamics. For a judicious modelling of the evolution of a fluid flow, the noise term needs to be properly calibrated. Lagrangian methods have been developed in this sense, where particle trajectories are simulated starting from each point on both the physical grid and its refined version, then the differences between the particle positions are used to calibrate the noise. This is computationally expensive and not fully justified from a theoretical perspective. We propose an Eulerian alternative which is tested on a stochastic rotating shallow water system and it can be applied to a general class of stochastic models. This is joint work with Dan Crisan and Alex Lobbe and the results are being published in “Noise calibration for SPDEs: a case study for the rotating shallow water model” (Foundations of Data Science), arXiv:2305.03548.

Week 4. Thomas Hudson (Warwick) - Crystal evolution at the nanoscale: Elasticity, plasticity and dislocations

Dislocation motion is a key feature of crystal plasticity at the smallest scales, and many mathematical challenges must be overcome to establish accurate, well-posed theories which connect our knowledge about dislocation motion at the nanoscale with the predictive power of macroscopic models.

I will present a range of recent work with my Warwick-based collaborators on the formulation and fitting of a range of models at the interface between atomistic and continuum theories. The first of these works focuses on the formulation of a new space-time geometric model for dislocation motion with Filip Rindler. If time permits, I also hope to discuss ongoing work on the data-driven fitting and simulation of reduced models for dislocation motion, starting from both atomistic and continuum theories; the latter projects are work with Geraldine Anis, Peter Brommer, Joseph Duque Lopez and James Kermode.

Week 5. Edwina Yeo (UCL) - Crystal evolution at the nanoscale: Elasticity, plasticity and dislocations

A wide range of biological and therapeutic species change their behaviour, geometry or propensity to adhere in response to external stimuli. For instance, bacteria modify their swimming behaviour close to fluid boundaries and proteins unfold differently depending on local flow structure. Predicting the behaviour of these species in macroscale fluid flows is vital to mitigate and understand effects such as aggregation or surface adhesion.

In this talk, I will present two examples of incorporating discrete microscale behaviour into continuum models via mean-field modelling. Firstly, I include microscale protein unfolding to predict blood clot initiation and secondly, I include microscale magnetic interactions to predict the macroscale aggregation and transport of magnetic nanoparticles. I will discuss the benefits of upscaling for model parameterisation and prediction as well as the limitations of the resulting macroscale models.

Week 6. Luke Davis (UCL) - Active matter under control: Insights from response theory

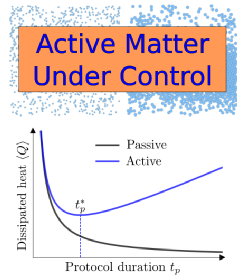
Active constituents burn fuel to sustain individual motion, giving rise to collective effects that are not seen in systems at thermal equilibrium, such as phase separation with purely repulsive interactions. There is a great potential in harnessing the striking phenomenology of active matter to build novel controllable and responsive materials that surpass passive ones. Yet, we currently lack a systematic roadmap to predict the protocols driving active systems between different states in a way that is thermodynamically optimal. Equilibrium thermodynamics is an inadequate foundation to this end, due to the dissipation rate arising from the constant fuel consumption in active matter. In this talk I will walk you through the key derivation steps and implementation of our versatile framework for the thermodynamic control of active matter. Combining recent developments in stochastic thermodynamics and nonequilibrium response theory, our approach shows how to find the optimal control for either continuous- or discrete-state active systems operating arbitrarily far from equilibrium. Our results open the door to designing novel active materials which are not only built to stabilize specific nonequilibrium collective states, but are also optimized to switch between different states at minimum dissipation.

Week 7. Boris Shraiman (UCSB) - Physics of Morphogenesis

Morphogenesis is a developmental process through which plants and animals acquire their shape and form. Although Biology has identified many of the key genes and cellular mechanisms of morphogenesis, the question of how Living Matter encodes the geometry of the shapes that it generates remains an open problem. This talk will focus on the interplay of physical forces and genetically encoded regulation that underly morphogenic processes. Specifically, the talk will describe how mechanical self-organization on cellular scale acts to convert spatial patterns of developmental gene expression into controlled transformation of tissue shape. We will see that i) simple ideas from Physics go far in explaining non-trivial behavior of tissues, and that ii) “active mechanics” encountered in tissue morphogenesis pushes the envelope of continuum mechanics beyond what we have learned from textbooks.

Week 8. Michael Faulkner (Warwick) - Fast sampling at phase transitions in statistical physics