Organisers
Giuseppe Cannizzaro and Vedran Sohinger
In Term 3, talks are held on Wednesdays 16-17 in B3.02.
Seminars in Term 1.
Oct 4- Tom Klose, University of Warwick
Title: Large deviations for the Φ^4_3 measure via Stochastic Quantisation
Abstract:
The Φ^4_3 measure is one of the easiest non-trivial examples of a Euclidean quantum field theory (EQFT) whose rigorous construction in the 1970's has been one of the celebrated achievements of the Constructive QFT community. In recent years, progress in the field of singular stochastic PDEs, initiated by the theory of regularity structures, has allowed for a new construction of the Φ^4_3 EQFT as the invariant measure of a previously ill-posed Langevin dynamics – a strategy originally proposed by Parisi and Wu ('81) under the name Stochastic Quantisation. In this talk, I will demonstrate that the same idea also allows to transfer the large deviation principle for the Φ^4_3 dynamics, obtained by Hairer and Weber ('15), to the corresponding EQFT. Our strategy is inspired by earlier works of Sowers ('92) and Cerrai and Röckner ('05) for non-singular dynamics and potentially also applies to other EQFT measures. This talk is based on joint work with Avi Mayorcas (University of Bath).
Oct 11- Ellen Powell, University of Durham
Title: Characterising the Gaussian free field
Abstract:
I will discuss recent approaches to characterising the Gaussian free field in the plane, and in higher dimensions. This is based on joint work with Juhan Aru, Nathanael Berestycki and Gourab Ray.
Oct 18- Anna Maltsev, Queen Mary University
Title: Bulk Universality for Complex Non-Hermitian Gauss-divisible Matrices
Abstract:
In this talk I will discuss universality of the k-point correlation function for Gauss divisible non-Hermitian matrices. We consider NxN matrices with centred, independent and identically distributed complex entries that have a small Gaussian component. We prove that the bulk correlation functions are universal in the large N limit using Householder transformations, supersymmetry, and Laplace method. Assuming the entries have finite moments and are supported on at least three points, the Gaussian component is removed by the four moment theorem. This is based on joint work with Mohammed Osman.
Oct 25- Julien Sabin, University of Rennes
Title: Nonlinear Hartree dynamics for density matrices
Abstract: In this talk I will review results concerning the mean-field dynamics of fermionic quantum particles governed by the nonlinear Hartree equation. The particularity of this equation is that its unknown is a bounded operator on a Hilbert space, rather than a (wave)function as is the case for most PDEs. I will explain how to deal with setting, with a focus on the large time behaviour of solutions.
Nov 1- Erlend Grong, University of Bergen
Title: Sub-Riemannian geometry, most probable paths and transformations.
Abstract: Doing statistics on a Riemannian manifold becomes very complicated for the reason that we lack tools to define such things as mean and variance. Using the Riemannian distance, we can define a mean know as the Fréchet mean, but this gives no concept of asymmetry, also known as anisotropy. We introduce an alternative definition of mean called the diffusion mean, which is able to both give a mean and the analogue of a covariance matrix for a dataset on a Riemannian manifolds.
Surprisingly, computing this mean and covariance is related to sub-Riemannian geometry. We describe how sub-Riemannian geometry can be applied in this setting, and mention some finite dimensional and infinite-dimensional applications.
The results are part of joint work with Stefan Sommer (Copenhagen, Denmark)
Nov 8- Balint Toth, University of Bristol
Title: (Towards an) Invariance Principle for the Random Lorentz Gas under Weak Coupling Limit Beyond the Kinetic Time Scale
Abstract: Kesten-Papanicolaou (1980) proved that in the weak coupling limit the random Lorentz-gas process with soft scatterers converges to the Spherical Langevin Process. Under a second, diffusive limit the spatial component of the Spherical Langevin Process converges to Brownian motion. Komorowski-Ryzhik (2006) proved that combining the weak coupling and diffusive limits, the Brownian motion is obtained, at least for a time horizon slightly beyond the kinetic time-scale. We attempt to extend this last result robustly for time scales way beyond the kinetic one. (Work in progress.)
Nov 15- Luisa Andreis, Politecnico di Milano
Title: Spatial coagulation processes: large deviations and phase transitions.
Abstract: We consider a spatial Markovian particle system with pairwise coagulation: after independent exponential random times, particle pairs merge into a single particle, and their masses are summed. We derive an explicit formula for the joint distribution of the particle configuration at a given fixed time, which involves the binary trees describing the history of how each of the particles has been formed via coagulations. While usually these processes are studied with the help of PDE (generalisation of the well-known Smoluchowski equation), our approach comes from statistical mechanics. The description is indeed in terms of a reference process, a Poisson point process of point group distributions, where each of the histories is an independent tree, and the non-coagulation between any two of them induces an exponential pair-interaction. Based on this formula, we can give a (conditional) large-deviation principle for the joint distribution of the particle histories in the limit of many particles with explicit identification of the rate function. We characterise its minimizer(s) and give criteria for the occurrence of a gelation phase transition, i.e., a loss of mass in the limiting configuration. This talk is based on an ongoing joint work with W. König, H. Langhammer and R.I.A. Patterson (WIAS Berlin).
Nov 22- Cristoforos Panagiotis, University of Bath
Title: Quantitative sub-ballisticity of self-avoiding walk on the hexagonal lattice
Abstract: In this talk, we will consider the self-avoiding walk on the hexagonal lattice, which is one of the few lattices whose connective constant can be computed explicitly. This was proved by Duminil-Copin and Smirnov in 2012 when they introduced the parafermionic observable. In this talk, we will use the observable to show that, with high probability, a self-avoiding walk of length n does not exit a ball of radius n/logn. This improves on an earlier result of Duminil-Copin and Hammond, who obtained a non-quantitative o(n) bound. Along the way, we show that at criticality, the partition function of bridges of height T decays polynomially fast to 0. Joint work with Dmitrii Krachun.
Nov 29- Marielle Simon, University of Lyon
Title: A few scaling limits results for the facilitated exclusion process in 1d
Abstract: The aim of this talk is to present some recent results which have been obtained for the facilitated exclusion process in one dimension. This stochastic lattice gas is subject to strong kinetic constraints which create a continuous phase transition to an absorbing state at a critical value of the particle density. If the microscopic dynamics is symmetric, its macroscopic behavior, under periodic boundary conditions and diffusive time scaling, is ruled by a non-linear PDE belonging to free boundary problems (or Stefan problems). One of the ingredients is to show that the system typically reaches an ergodic component in subdiffusive time.
The asymmetric case can also be fully treated: in this case, considered on the infinite line, the empirical density converges to the unique entropy solution to a hyperbolic Stefan problem. All these results rely, to various extent, on a mapping argument with a zero-range process, which completely fails in dimension higher than 1.
Based on joint works with O. Blondel, C. Erignoux, M. Sasada and L. Zhao.
Dec 6- Ilya Chevyrev, University of Edinburgh
Title: Decorated path spaces with applications to fast-slow systems
Abstract: In this talk, I will present a space of decorated paths that allows one to keep track of oscillations of paths that happens in infinitesimal time. Despite its simple definition as a naive completion of the Skorokhod space, this notion is fruitful in the study of ordinary differential equations with jumps, generalising the framework of Marcus, and applies in situations where classical Skorokhod topologies are too restrictive. As an application, I will show how homogenisation theorems of superdiffusive fast-slow systems, including billiards with flat cusps, can be stated and proved in this framework. Based on a joint work with Alexey Korepanov and Ian Melbourne.
Term 2
Jan 17-Tamara Grava (University of Bristol)
Title: A soliton gas for the focusing nonlinear Schrödinger equation
Abstract: We consider the focusing nonlinear Schrödinger equation on the line. This equation admits a N soliton solution parametrised by 2N complex spectral data. In recent years many significant numerical simulations that study large sets of random solitons have been realised. We consider a random configuration of N solitons with respect to a probability distributions on the spectral data. We then show that the N soliton solution, after suitable rescalings converges to a normal distribution as N goes to infinity.
Jan 24- Sandro Franceschi (Polytechnique Paris)
Title: Reflected Brownian motion in a cone: a study of the transient case.
Abstract: One of the classic problems in the literature devoted to reflected Brownian motion in a two-dimensional cone is the study of its stationary distribution in the recurrent case. On the other hand, we will focus in this talk on the transient case to study the Green's functions of this process and their asymptotics. This will naturally lead us to consider the Martin boundary of the process which allows us to determine the harmonic functions satisfying oblique Neumann conditions on the edges. For some models, we will illustrate this by studying the probability of escape of the process along an axis or its probability of absorption at the origin.
To establish our results, we use analytical methods historically developed in probability and combinatorics to study random walks in the quadrant. We establish functional equations satisfied by the Laplace transforms of Green's functions and the probabilities of escape or absorption. Thanks to the theory of boundary value problems (of Riemann and Carleman) it is possible to determine explicit formulas for these transforms involving hypergeometric functions. The saddle point method and transfer lemmas enable us to obtain asymptotic results and establish the Martin boundary.
(NOTE DIFFERENT DAY, TIME, AND PLACE) Feb 1: talk moved to Statistical Mechanics Seminar slot, 14-15, MS.03- Markus Tempelmeyr (Münster Universität)
Title: Malliavin calculus and regularity structures
Abstract:
We give an overview of some probabilistic aspects of the solution theory for singular SPDEs, following the recent approach of Otto, Sauer, Smith and Weber. The basic idea is to parameterize the model, which captures the local solution behaviour, by partial derivatives w.r.t. the nonlinearity. Malliavin calculus plays a prominent role, on the one hand to obtain convergence of renormalized models based on a spectral gap assumption of the driving noise, on the other hand to obtain a characterization of models establishing a universality-type result. Based on joint work with Lucas Broux, Pablo Linares, Felix Otto and Pavlos Tsatsoulis.
Feb 7- Perla Sousi (University of Cambridge)
Title: Phase transition for the late points of random walk
Abstract: Let
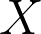
be a simple random walk in

with
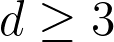
and let

be the expected time it takes for
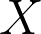
to visit all vertices of the torus. In joint work with Prévost and Rodriguez we study the set

of points that have not been visited by time
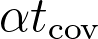
and prove that it exhibits a phase transition: there exists
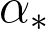
so that for all

and all

there exists a coupling between

and two i.i.d. Bernoulli sets
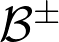
on the torus with parameters
d%7D)
with the property that
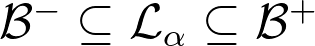
with probability tending to 1 as
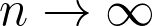
. When
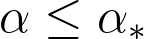
, we prove that there is no such coupling.
Feb 14- Peter Morfe (Max-Planck Institut, Leipzig)
Title: Anomalous Diffusion for a Passive Tracer Advected by the Curl of the 2D GFF
Abstract: I will describe recent work on anomalous diffusion asymptotics for diffusions advected by turbulent velocity fields. Precisely, the model of interest involves a passive tracer subjected to Brownian diffusion and advection by the curl of the Gaussian free field (or divergence-free white noise). Recent work of Cannizzaro, Haunschmidt-Sibitz, and
Toninelli (2022) established that the mean-square displacement is borderline superdiffusive with a logarithmic correction, confirming earlier predictions of the physics literature and a conjecture of Toth and Valko (2011). In joint work with Chatzigeorgiou, Otto, and Wang, we give an alternative proof built around ideas from stochastic homogenization, with a slightly stronger conclusion.
Feb 21- Sabine Jansen (LMU)
Title: Cluster expansions & Kirkwood-Salsburg: 2-body vs. multi-body interactions
Abstract: Cluster expansions give power series expansions in statistical mechanics, for example, for correlation functions (factorial moment densities) or the pressure of a classical gas at low density in a grand-canonical Gibbs measure (Gibbs point process). The series captures corrections towards the ideal gas (Poisson point process). I will present an abstract if and only if convergence condition for non-negative pair potentials based on the Kirkwood-Salsburg equations (joint work with Leonid Kolesnikov) and present some challenges and ideas for multi-body interactions.
Feb 28- We have two seminars this week. Note the room change.
First seminar (16-17, B3.02) Cecile Mailler (University of Bath)
Title: A two-table theorem for a disordered version of the Chinese restaurant process (CRP).
Abstract: In this joint work with Jakob Björnberg, Peter Mörters and Daniel Ueltschi, we introduce a disordered version of the CRP in which tables have different weights (or fitnesses). When a new customer enters the restaurant, they choose to open a new table with probability proportional to a parameter $\theta$, or they sit at an occupied table with probability proportional to the weight of this table times the number of customers already sitting at this table. We show that, in this model, in probability, a proportion converging to one of all customers sit at the largest table. We also show that this is not true almost surely, but prove instead that, almost surely, a proportion converging to one of all customers sit at one of the two largest tables.
Second seminar (17-18, B3.02) Ron Peled (Tel Aviv University)
Title: Minimal Surfaces in Random Environment
Abstract: A minimal surface in a random environment (MSRE) is a surface which minimizes the sum of its elastic energy and its environment potential energy, subject to prescribed boundary conditions. Apart from their intrinsic interest, such surfaces are further motivated by connections with disordered spin systems, first-passage percolation models and minimal cuts in the Z^D lattice with random capacities.
We wish to study the geometry of d-dimensional minimal surfaces in a (d+n)-dimensional random environment. Specializing to a model that we term harmonic MSRE, in an ``independent'' random environment, we rigorously establish bounds on the geometric and energetic fluctuations of the minimal surface, as well as a scaling relation that ties together these two types of fluctuations. In particular, we prove, for all values of n, that the surfaces are delocalized in dimensions d≤4 and localized in dimensions d≥5. Moreover, the surface delocalizes with power-law fluctuations when d≤3 and with sub-power-law fluctuations when d=4. Many of our results are new even for d=1 (indeed, even for d=n=1), corresponding to the well-studied case of (non-integrable) first-passage percolation.
No prior knowledge in the topic will be assumed.
Based on joint work with Barbara Dembin, Dor Elboim and Daniel Hadas. Joint work with Michal Bassan and Shoni Gilboa will also be discussed.
Mar 3- Ana Djurdjevac (Freie Universität Berlin) Room change: The seminar will take place in B3.02
Title: Nonlinear SPDE models of particle systems
Abstract: Interacting particle systems provide flexible and powerful models that are useful in many application areas such as sociology (agents), molecular dynamics (proteins) etc. However, particle systems with large numbers of particles are very complex and diffcult to handle, both analytically and computationally. Therefore, a common strategy is to derive effective equations that describe the time evolution of the empirical particle density. An example
of such equations is the well-studied singular Dean-Kawasaki equation. We will introduce nonlinear and non-Gaussian models that provide approximation of the evolution of the empirical density of a given particle system. The well-posedness result of the approximated nonlinear SPDE in the case of independent particles is a joint work with H. Kremp and N. Perkowski. Furthermore, we want to study numerical approximation of those type of
nonlinear SPDEs. In particular, since the unknown is the empirical density, the main goal is to provide numerical methods that preserve positivity. For that purpose we are considering the so called hybrid methods. This is a
joint work with J. Bell and A. Almgren.
Mar 13- Ioannis Karatzas (Columbia University)
Title: Conservative diffusions and Markov chains as entropic flows of steepest descent
Abstract: We provide a detailed, probabilistic interpretation for the variational characterization of conservative diffusions as entropic flows of steepest descent. Jordan, Kinderlehrer and Otto showed in 1998, via a numerical scheme, that for diffusions of Langevin-Smoluchowski type the Fokker-Planck probability density flow minimizes the rate of relative entropy dissipation, as measured by the distance traveled in terms of the quadratic Wasserstein metric in the ambient space of configurations. Using a very direct perturbation analysis we obtain novel, stochastic-process versions of such features; these are valid along almost every trajectory of the motion in both the forward and, most transparently, the backward, directions of time. The original results follow then simply by “aggregating”, i.e., taking expectations. As a bonus we obtain a version of the HWI inequality of Otto and Villani, relating relative entropy, Fisher information, and Wasserstein distance. Similar results are outlined for reversible Markov Chains.
(Joint work with W. Schachermayer, B. Tschiderer and J. Maas, from Vienna.)
Term 3: Seminars take place on Wednesdays 16-17 in B3.02
24/04-Sarah-Jean Meyer (University of Oxford)
Title: The FBSDE approach to sine-Gordon up to $6\pi$.
Abstract:
I will present a stochastic analysis of the sine-Gordon Euclidean quantum field $(\cos(\beta\phi))_2$ on the full space up to the second threshold, i.e. for $\beta^2<6\pi$. The basis of our method is a stochastic quantisation equation given by a forward-backward stochastic differential equation (FBSDE) for a decomposition $(X_t)_(t\geq0)$ of the interacting Euclidean field $X_\infty$ along a scale parameter $t\geq0$ using an approximate version of the renormalisation flow equation. The FBSDE produces a scale-by-scale coupling of the interacting field with the Gaussian free field without cut-offs and describes the optimiser of a stochastic control problem for Euclidean QFTs introduced by Barashkov and Gubinelli. I will first explain the general set-up for the FBSDE approach. In the case of the sine-Gordon model, I will mention some applications of the FBSDE to illustrate that it can be used effectively to obtain results about large deviations, integrability, decay of correlations for local observables, singularity with respect to the free field, Osterwalder-Schrader axioms and other properties. This is joint work with Massimiliano Gubinelli.
01/05- William Fitzgerald (University of Manchester)
Title: Ordered random walks and the Airy line ensemble
Abstract: Consider a collection of one-dimensional random walks which are conditioned to remain in the same order for all time. This system has been named ordered random walks, non-intersecting/non-colliding random walks or vicious walkers.
Ordered random walks have many connections including with last passage percolation, interacting particle systems and random matrices. I will describe some of these connections and the behaviour as the number of walkers grows to infinity. This is based on joint work with Denis Denisov and Vitali Wachtel.
08/05- Francesca Cottini (University of Luxembourg)
Title: (Ir)reducible central limit theorems for polynomial chaos via spectral graph theory
Abstract: In this talk, we will first present a central limit theorem (CLT), based only on second moment assumptions, for polynomial chaos, i.e. multilinear polynomials of independent random variables. This reducible CLT (as it can be reduced to the application of a classical result by Feller-Lindeberg) finds its main application in the theory of 2d directed polymers and the related 2d Stochastic Heat Equation.
Among the class of polynomial chaos satisfying a universal CLT (according to Nourdin, Peccati, Reinart and their celebrated Fourth Moment Theorem), we will exhibit a sufficient condition for a polynomial chaos to be irreducible, i.e. it does not satisfy our reducible CLT via second moment only. The novelty of our approach and findings lies in the interpretation we offer solely based on the spectral and connectivity properties of relevant associated graphs and hypergraphs.
The talk is based on an ongoing project with Francesco Caravenna (Milano-Bicocca) and Giovanni Peccati (Luxembourg).
15/05- Brune Massoulié (Dauphine University)
Title: Cutoff for the transience time of the Facilitated Exclusion Process
Abstract: The facilitated exclusion process (FEP) is a particle system, where particles evolve on a discrete lattice, making random jumps while obeying local constraints. Because of these constraints, the process will almost surely become blocked (frozen), or reach an absorbing set of configurations after a finite time. This process can thus be seen as a toy model for the liquid-solid transition. In our work, we study the timescale after which these events occur, by introducing a new representation of this process. We therefore study a nonreversible variant of the simple symmetric exclusion process (SSEP), where particles can be destroyed by traps. This allows to make precise estimates on the transience time of both the FEP and the SSEP with traps, we also establish cutoff for the mixing time of the latter, and this opens the way for estimating precisely the mixing time of the FEP.
22/05-
29/05- SEMINAR CANCELLED
05/06- Louis-Pierre Arguin (University of Oxford)
Title: Large Values of the Riemann Zeta Function: A Probabilistic Approach
Abstract: I will give an account of the recent progress in probability and in number theory to understand the large values of the zeta function on the critical line, especially in short intervals. The problems have interesting connections to statistical mechanics of disordered systems, both in their interpretations and in the techniques of proofs. These connections will be emphasized. This is based in part on joint works with Emma Bailey, and with Paul Bourgade & Maksym Radziwill.
12/06-
19/06- Richard Kraaij (TU Delft)
Title: Well-posedness for Hamilton-Jacobi equations for stochastic control problems:
A new view on the classical approach using couplings
Abstract: Stochastic control problems for controlled Markov processes can be infinitesimally characterized using a second order Hamilton-Jacobi-Bellman (HJB) equation.
The classical work of Crandall-Ishii-Lions (1992) establishes how to obtain uniqueness of viscosity solutions for controlled diffusion processes, and a collection of recent works has pushed the estimates to include classes of spatially inhomogeneous controlled Lévy processes.
We introduce a new perspective of the classical proof methods in terms of Markovian couplings, enabling the extendion of the applicability to a wider range of Lévy type processes and paving the pay for extensions to new contexts.
Based on joint work (in progress) with Serena Della Corte (Delft), Fabian Fuchs (Bielefeld) and Max Nendel (Bielefeld).
26/06- SEMINAR CANCELLED
