Phonons
A phonon is the elementary excitation in the quantum mechanical treatment of vibrations in a crystal lattice [1] or the quantum unit of a crystal lattice vibration.
They are analogous to photons, having energy of ћω as quanta of excitation of the lattice vibration mode of angular frequency ω. Since the momentum ћk is exact, by the uncertainty principle, the position of phonons cannot be determined, and so, phonons are not localized particles. Nevertheless, just like the case with photons or electrons, a fairly localized wavepacket can be constructed by combining modes of slightly different frequency and wavelength. By taking waves with a spread of k of order π/10a, a wavepacket localized within about 10 unit cells are made, representing a fairly localized phonon with group velocity dω/dk; within the limits of the uncertainty principle.
Although it is convenient to interpret ћk as the phonon momentum, it is not really the true kinematic momentum and often referred to as ‘crystal momentum’. In a 1D crystal lattice, a lattice mode with wavenumber k can be equally represented by a wavenumber k + 2πn/a. Therefore, it is not possible to give a unique value of k to a phonon.
Like photons, phonons are bosons and not conserved; they can be created or destroyed in collisions. Phonons, through emission or absorption, scatter inelastically with neutrons by experiment and determines the phonon dispersion relations ω(k). The ω(k) curve for lattice vibrations can be interpreted with both axes multiplied by ћ, as a relation between energy and momentum for phonons ( E = ћω, p = ћk ). Phonon dispersion relation shows features in crystals with two or more atoms per primitive basis.
If a phonon with wavevector is created by inelastic scattering of a photon or neutron from wavevector
to
, the wavevector selection rule that governs the process [2] is
Where is a reciprocal lattice vector
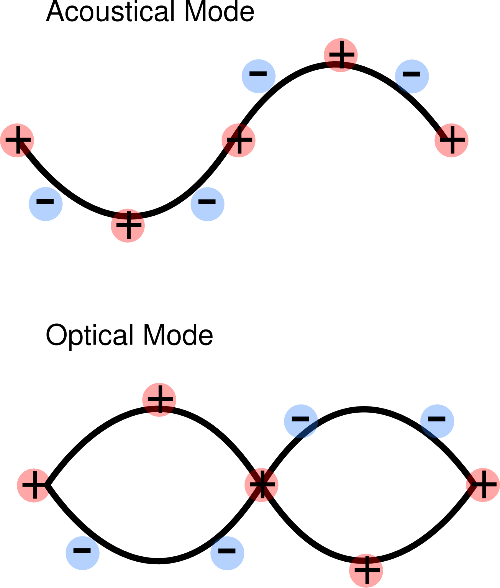
Acoustic Phonons and optical phonons
When the unit cell contains more than one atom, the crystal will contain two types of phonon, acoustic and optical. Optical phonons are excited easily by light. In acoustic phonons, both positive and negative ions swing together. In optical phonons, positive and negative phonons swing against each other.
Phonon Energy
If the angular frequency of a phonon is given by ω, then the energy of the phonon is [2]
Phonon-phonon collision
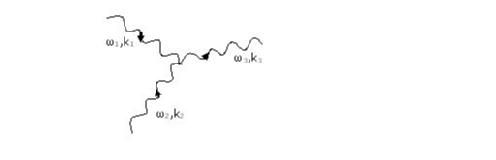
Fig 2: A collision where phonon 1 and 2 coalesce to give phonon 3.
In figure 2, a phonon of wavenumber k1 and frequency ω1 coalesces with a phonon of wavenumber k2 and frequency ω2 to produce phonon 3 with wavenumber k3 and frequency ω3.
editted by Wan Maryam Wan Ahmad Kamil
Refference
1.
2. Introduction to slid state physics, Kittel.
3. Solid State Physics, J.R.Hook and H.E.Hall
