I work in the field of soft matter theory, on problems ranging from the topological properties of ordered media and colloids in liquid crystals to low Reynolds number motility and collective behaviour in soft active matter. Running through all of these things is my particular interest in the application, and development, of topological, or geometrical, techniques to problems in physics.

Group

I am currently working with Alex Houston (start 2017) on Active Liquid Crystals and VJ Pratley (start 2020) on Three-Dimensional Active Matter. I am also cosupervising SJ Kole (start 2019; student with Sriram Ramaswamy at Indian Institute of Science) on Geometry and Chirality in Active Liquid Crystals.

URSS Projects: I am usually happy to offer a URSS project for a capable student (in the summer before their fourth year) wishing to get an insight into modern theoretical physics or applied mathematics.

News

Tuesday 1st December 2020: Congratulations to Joe Pollard for successfully defending his thesis!! (and thanks to Randy Kamien and Robert MacKay as examiners)

Monday 8th July 2019: Congratulations to Jack Binysh for successfully defending his thesis!! (and thanks to Paul Sutcliffe and Matthew Turner as examiners)

Monday 4th June 2018: Congratulations to former student Tom Machon for winning the 2018 Glenn H Brown Prize of the International Liquid Crystal Society, "For the advancement of geometric and topological methods in the theory of liquid crystals, especially in the description of knotted disclinations and the global homotopy classification of nematic textures"

Wednesday 27th September 2017: Congratulations to Joel Nicholls for successfully defending his thesis!! (and thanks to Sebastian Ahnert and Robin Ball as examiners)

Monday 26th June 2017: Congratulations to Diana Khoromskaia for successfully defending her thesis!! (and thanks to Rhoda Hawkins and Matthew Turner as examiners)

Thursday 23rd March 2017: Congratulations to Jack Binysh on being awarded a David Crighton Fellowship! Jack will hold the fellowship in DAMTP, hosted by Ray Goldstein

Thursday 22nd September 2016: Congratulations to Dario Papavassiliou for successfully defending his thesis!! (and thanks to Julia Yeomans and Robin Ball as examiners)

Tuesday 31st May 2016: Congratulations to Tom Machon for winning a Faculty of Science PhD Thesis Prize!

Monday 8th February 2016: Welcome to Carl Whitfield, who joins us as a postdoc.

Thursday 10th December 2015: Congratulations to Tom Machon for successfully defending his thesis!! (and thanks to Mark Dennis and Matthew Turner as examiners)

Past group members

 Davide Michieletto (PhD 2015, supervisor Matthew Turner), now Royal Society URF at Edinburgh

Tom Machon (PhD 2016, Aspects of Geometry and Topology in Liquid Crystalline Phases), now Lecturer in Theoretical Physics at Bristol

Anja Humpert (PhD 2016, supervisor Mike Allen), now Software Engineer at Waters Corporation

Dario Papavassiliou (PhD 2016, The Reciprocal Theorem and Swimmer Interactions), now maths and physics teacher

Carl Whitfield (Postdoc 2016), now postdoc at Manchester

Diana Khoromskaia (PhD 2017, Active Liquid Crystals in Confined Geometries), now postdoc at the Francis Crick Institute

Joel Nicholls (PhD 2017, Polyomino Models of Molecular Monolayers), now Deep Learning Researcher at LeapMind (Tokyo)

Jack Binysh (PhD 2019, Construction and Dynamics of Knotted Fields in Soft Matter Systems), now postdoc with Anton Souslov at Bath

Joe Pollard (PhD 2020, The Topology and Geometry of Liquid Crystals), now postdoc with Suzanne Fielding at Durham

We have weekly group meetings in soft matter physics with Matthew Turner, Marco Polin, Vasily Kantsler and Robin Ball -- the current schedule is available here.

Latest publications

Geometry of Bend: Singular Lines and Defects in Twist-Bend Nematics

Jack Binysh, Joseph Pollard, and Gareth P. Alexander, Phys. Rev. Lett. 125, 047801 (2020). Open Access

We describe the geometry of bend distortions in twist-bend nematic liquid crystals in terms of their fundamental degeneracies, which we call β lines. These represent a new class of line-like topological defect. We use them to construct and characterise novel structures, including grain boundary and focal conic smectic-like defects, Skyrmions, and knotted merons. We analyse their local geometry and global structure, showing that their intersection with any surface is twice the Skyrmion number. Finally, we demonstrate how arbitrary knots and links can be created and describe them in terms of merons, giving a new geometric perspective on the fractionalisation of Skyrmions.

Preprint: arXiv:2002.00916 [cond-mat.soft].

A Björling Representation for Jacobi Fields on Minimal Surfaces and Soap Film Instabilities

Gareth P. Alexander and Thomas Machon, Proc. R. Soc. A 476, 20190903 (2020).

We develop a general framework for the description of instabilities on soap films using the Björling representation of minimal surfaces. The construction is naturally geometric and the instability has the interpretation as being specified by its amplitude and transverse gradient along any curve lying in the minimal surface. When the amplitude vanishes, the curve forms part of the boundary to a critically stable domain, while when the gradient vanishes the Jacobi field is maximal along the curve. In the latter case, we show that the Jacobi field is maximally localised if its amplitude is taken to be the lowest eigenfunction of a one-dimensional Schrödinger operator. We present examples for the helicoid, catenoid, circular helicoids and planar Enneper minimal surfaces, and emphasise that the geometric nature of the Björling representation allows direct connection with instabilities observed in soap films.

Preprint: arXiv:1912.13009 [cond-mat.soft].

Singular Contact Geometry and Beltrami Fields in Cholesteric Liquid Crystals

Joseph Pollard and Gareth P. Alexander

The description of point defects in chiral liquid crystals via topological methods requires the introduction of singular contact structures, a generalisation of regular contact structures where the plane field may have singularities at isolated points. We characterise the class of singularities that may arise in such structures, as well as the subclass of singularities that can occur in a Beltrami field. We discuss questions of global existence, and prove that all singular contact structures with nonremovable singularities are overtwisted. To connect the theory to experiment we also discuss normal and tangential boundary conditions for singular contact structures, and show we can realise all desired boundary conditions except for normal anchoring on a sphere, where a theorem of Eliashberg and Thurston provides an obstruction to having a singular contact structure in the interior. By introducing a singular version of the Lutz twist we show that all contact structures are homotopic within the larger class of singular contact structures. We give applications of our results to the description of topological defects in chiral liquid crystals.

Preprint: arXiv:1911.10159 [math.SG].

Three-Dimensional Active Defect Loops

Jack Binysh, Žiga Kos, Simon Čopar, Miha Ravnik, and Gareth P. Alexander, Phys. Rev. Lett. 124, 088001 (2020). Open Access

We describe the flows and morphological dynamics of topological defect lines and loops in three-dimensional active nematics and show, using theory and numerical modelling, that they are governed by the local profile of the orientational order surrounding the defects. Analysing a continuous span of defect loop profiles, ranging from radial and tangential twist to wedge ±1/2 profiles, we show that the distinct geometries can drive material flow perpendicular or along the local defect loop segment, whose variation around a closed loop can lead to net loop motion, elongation or compression of shape, or buckling of the loops. We demonstrate a correlation between local curvature and the local orientational profile of the defect loop, indicating dynamic coupling between geometry and topology. To address the general formation of defect loops in three dimensions, we show their creation via bend instability from different initial elastic distortions.

Preprint: arXiv:1909.07109 [cond-mat.soft].

Stable and Unstable Vortex Knots in Excitable Media

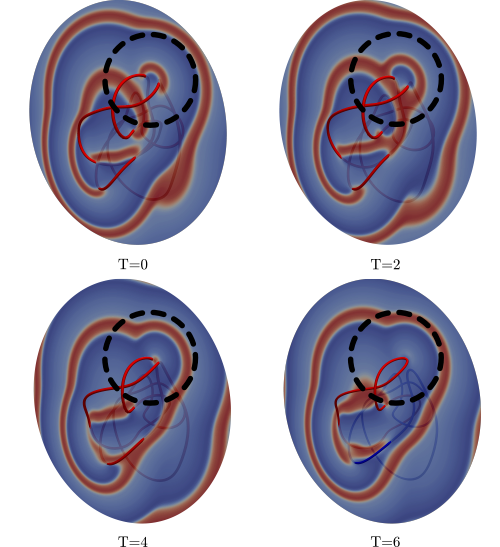
Jack Binysh, Carl A. Whitfield, and Gareth P. Alexander, Phys. Rev. E 99, 012211 (2019). Open Access

We study the dynamics of knotted vortices in a bulk excitable medium using the FitzHugh-Nagumo model. From a systematic survey of all knots of at most eight crossings we establish that the generic behaviour is of unsteady, irregular dynamics, with prolonged periods of expansion of parts of the vortex. The mechanism for the length expansion is a long-range 'wave slapping' interaction, analogous to that responsible for the annihilation of small vortex rings by larger ones. We also show that there are stable vortex geometries for certain knots; in addition to the unknot, trefoil and figure eight knots reported previously, we have found stable examples of the Whitehead link and 6₂ knot. We give a thorough characterisation of their geometry and steady state motion. For the unknot, trefoil and figure eight knots we greatly expand previous evidence that FitzHugh-Nagumo dynamics untangles initially complex geometries while preserving topology.

Preprint: arXiv:1809.04567 [nlin.PS].

Point Defects, Topological Chirality and Singularity Theory in Cholesteric Liquid Crystal Droplets

Joseph Pollard, Gregor Posnjak, Simon Čopar, Igor Muševič, and Gareth P. Alexander, Phys. Rev. X 9, 021004 (2019). Open Access

We provide a characterisation of point defects in droplets of cholesteric liquid crystal, using a combination of experiment, simulation and theoretical analysis. These droplets display a range of structures including realisations of defects with high topological charge and arrangements of multiple defects in 'topological molecules'. We show that there are certain defects that are incompatible with a uniform sense of chiral twisting for topological reasons. Furthermore, those defects that are compatible with twist of a single handedness are shown to have the structure of the gradient field of an isolated critical point and hence are described by singularity theory. We show that the mathematical tools of singularity theory reproduce, with excellent agreement, the experimental observations of high charge defects and topological molecules. Our results have implications beyond liquid crystal droplets in characterising chiral materials and their topology in general.

Preprint: arXiv:1808.03492 [cond-mat.soft].

Woven Nematic Defects, Skyrmions, and the Abelian Sandpile Model

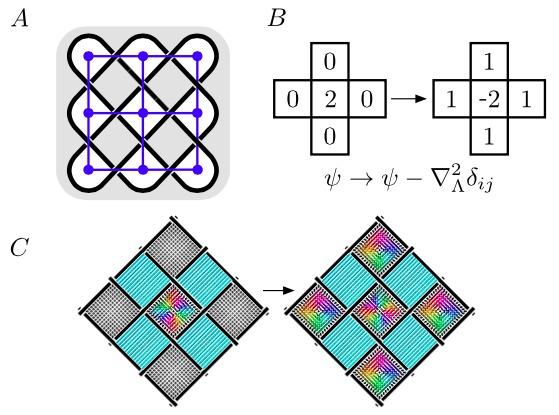
Thomas Machon and Gareth P. Alexander, Phys. Rev. Lett. 121, 237801 (2018).

We show that a fixed set of woven defect lines in a nematic liquid crystal supports a set of non-singular topological states which can be mapped on to recurrent stable configurations in the Abelian sandpile model or chip-firing game. The physical correspondence between local Skyrmion flux and sandpile height is made between the two models. Using a toy model of the elastic energy, we examine the structure of energy minima as a function of topological class and show that the system admits domain wall Skyrmion solitons.

Preprint: arXiv:1808.02425 [cond-mat.soft].

Maxwell's Theory of Solid Angle and the Construction of Knotted Fields

Jack Binysh and Gareth P. Alexander, J. Phys. A: Math. Theor. 51, 385202 (2018). Open Access

We provide a systematic description of the solid angle function as a means of constructing a knotted field for any curve or link in R³. This is a purely geometric construction in which all of the properties of the entire knotted field derive from the geometry of the curve, and from projective and spherical geometry. We emphasise a fundamental homotopy formula as unifying different formulae for computing the solid angle. The solid angle induces a natural framing of the curve, which we show is related to its writhe and use to characterise the local structure in a neighbourhood of the knot. Finally, we discuss computational implementation of the formulae derived, with C code provided, and give illustrations for how the solid angle may be used to give explicit constructions of knotted scroll waves in excitable media and knotted director fields around disclination lines in nematic liquid crystals.

C code developed as part of this work is freely available at github.com/garethalexander

Preprint: arXiv:1805.10358 [math-ph].

Vortex formation and dynamics of defects in active nematic shells

Diana Khoromskaia and Gareth P. Alexander, New J. Phys. 19, 103043 (2017). Open Access

We present a hydrodynamic model for a thin spherical shell of active nematic liquid crystal with an arbitrary configuration of defects. The active flows generated by defects in the director lead to the formation of stable vortices, analogous to those seen in confined systems in flat geometries, which generate an effective dynamics for four +1/2 defects that reproduces the tetrahedral to planar oscillations observed in experiments. As the activity is increased and the vortices become stronger, the defects are drawn more tightly into pairs, rotating about antipodal points. We extend this situation to also describe the dynamics of other configurations of defects. For example, two +1 defects are found to attract or repel according to the local geometric character of the director field around them, while additional pairs of opposite charge defects can give rise to flow states containing more than two vortices. Finally, we describe the generic relationship between defects in the orientation and singular points of the flow, and suggest implications for the three-dimensional nature of the flow and deformation in the shape of the shell.

Preprint: arXiv:1608.02813 [cond-mat.soft].

Straight Round the Twist: Frustration and Chirality in Smectics-A

Elisabetta A. Matsumoto, Randall D. Kamien, and Gareth P. Alexander, Interface Focus 7: 20160118 (2017).

Frustration is a powerful mechanism in condensed matter systems, driving both order and co plexity. In smectics, the frustration between macroscopic chirality and equally spaced layers generates textures characterised by a proliferation of defects. In this article, we study several different ground states of the chiral Landau-de Gennes free energy for a smectic liquid crystal. The standard theory finds the twist grain boundary (TGB) phase to be the ground state for chiral type II smectics. However, for very highly chiral systems, the hierarchical helical nanofilament (HN) phase can form and is stable over the TGB.

Preprint: arXiv:1611.03830 [cond-mat.soft].

Hydrodynamic instabilities in active cholesteric liquid crystals

Carl A. Whitfield, Tapan Chandra Adhyapak, Adriano Tiribocchi, Gareth P. Alexander, Davide Marenduzzo, and Sriram Ramaswamy, Eur. Phys. J. E 40: 50 (2017). Open Access

We describe the basic properties and consequences of introducing active stresses, with principal direction along the local director, in cholesteric liquid crystals. The helical ground state is found to be linearly unstable to extensile stresses, without threshold in the limit of infinite system size, whereas contractile stresses are hydrodynamically screened by the cholesteric elasticity to give a finite threshold. This is confirmed numerically and the non-linear consequences of instability, in both extensile and contractile cases, are studied. We also consider the stresses associated to defects in the cholesteric pitch (λ lines) and show how the geometry near to the defect generates threshold-less flows reminiscent of those for defects in active nematics. At large extensile activity λ lines are spontaneously created and can form steady state patterns sustained by constant active flows.

Preprint: arXiv:1701.05022 [cond-mat.soft].

Exact solutions for hydrodynamic interactions of two squirming spheres

Dario Papavassiliou and Gareth P. Alexander, J. Fluid Mech. 813, 618-646 (2017). Open Access

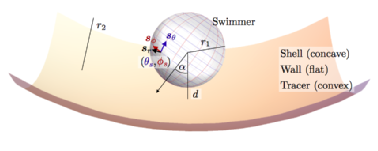
We provide exact solutions of the Stokes equations for a squirming sphere close to a no-slip surface, both planar and spherical, and for the interactions between two squirmers, in three dimensions. These allow the hydrodynamic interactions of swimming microscopic organisms with confining boundaries, or each other, to be determined for arbitrary separation and, in particular, in the close proximity regime where approximate methods based on point singularity descriptions cease to be valid. We give a detailed description of the circular motion of an arbitrary squirmer moving parallel to a no-slip spherical boundary or flat free surface at close separation, finding that the circling generically has opposite sense at free surfaces and at solid boundaries. While the asymptotic interaction is symmetric under head-tail reversal of the swimmer, in the near field microscopic structure can result in significant asymmetry. We also find the translational velocity towards the surface for a simple model with only the lowest two squirming modes. By comparing these to asymptotic approximations of the interaction we find that the transition from near- to far-field behaviour occurs at a separation of about two swimmer diameters. These solutions are for the rotational velocity about the wall normal, or common diameter of two spheres, and the translational speed along that same direction, and are obtained using the Lorentz reciprocal theorem for Stokes flows in conjunction with known solutions for the conjugate Stokes drag problems, the derivations of which are demonstrated here for completeness. The analogous motions in the perpendicular directions, i.e. parallel to the wall, currently cannot be calculated exactly since the relevant Stokes drag solutions needed for the reciprocal theorem are not available.

Preprint: arXiv:1602.06912 [physics.flu-dyn].

Instabilities and Solitons in Minimal Strips

Thomas Machon, Gareth P. Alexander, Raymond E. Goldstein, and Adriana I. Pesci, Phys. Rev. Lett. 117, 017801 (2016). Open Access

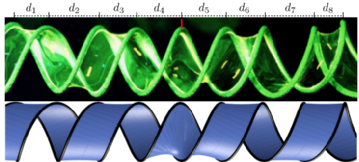We show that highly twisted minimal strips can undergo a non-singular transition, unlike the singular transitions seen in the Möbius strip and the catenoid. If the strip is non-orientable this transition is topologically frustrated, and the resulting surface contains a helical defect. Through a controlled analytic approximation the system can be mapped onto a scalar ϕ⁴ theory on a non-orientable line bundle over the circle, where the defect becomes a topologically protected kink soliton or domain wall, thus establishing their existence in minimal surfaces. Experimental studies of soap films confirm these results and demonstrate how the position of the defect can be controlled through boundary deformation.

Preprint: arXiv:1602.02652 [cond-mat.soft].

Global Theory of Defects in Nematic Liquid Crystals

Thomas Machon and Gareth P. Alexander, Proc. R. Soc. A 472, 20160265 (2016). Open Access

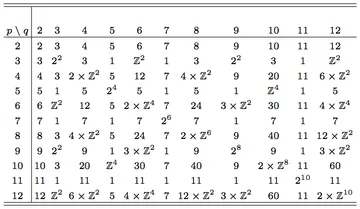We give the global homotopy classification of nematic textures for a general domain with weak anchoring boundary conditions and arbitrary defect set in terms of twisted cohomology, and give an explicit computation for the case of knotted and linked defects in R³, showing that the distinct homotopy classes have a 1-1 correspondence with the first homology group of the branched double cover, branched over the disclination loops. We show further that the subset of those classes corresponding to elements of order 2 in this group have representatives that are planar and characterise the obstruction for other classes in terms of merons. The planar textures are a feature of the global defect topology that is not reflected in any local characterisation. Finally, we describe how the global classification relates to recent experiments on nematic droplets and how elements of order 4 relate to the presence of τ lines in cholesterics.

Preprint: arXiv:1604.03429 [cond-mat.soft].

Umbilic Lines in Orientational Order

Thomas Machon and Gareth P. Alexander, Phys. Rev. X 6, 011033 (2016). Open Access

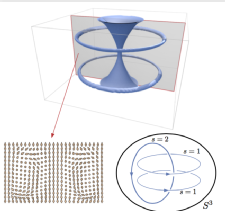
Three-dimensional orientational order in systems whose ground states possess non-zero, chiral gradients typically exhibits line-like structures or defects: λ lines in cholesterics or Skyrmion tubes in ferromagnets for example. Here we show that such lines can be identified as a set of natural geometric singularities in a unit vector field, the generalisation of the umbilic points of a surface. We characterise these lines in terms of the natural vector bundles that the order defines and show that they give a way to localise and identify Skyrmion distortions in chiral materials -- in particular that they supply a natural representative of the Poincaré dual of the cocycle describing the topology. Their global structure leads to the definition of a self-linking number and helicity integral which relates the linking of umbilic lines to the Hopf invariant of the texture.

Preprint: arXiv:1507.08875 [cond-mat.soft].

Motility of Active Fluid Drops on Surfaces

Diana Khoromskaia and Gareth P. Alexander, Phys. Rev. E 92, 062311 (2015). Open Access

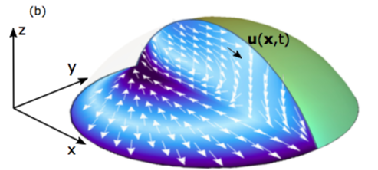Drops of active liquid crystal have recently shown the ability to self-propel, which was associated with topological defects in the orientation of active filaments [Sanchez et al., Nature 491, 431 (2013)]. Here, we study the onset and different aspects of motility of a three-dimensional drop of active fluid on a planar surface. We analyse theoretically how motility is affected by orientation profiles with defects of various types and locations, by the shape of the drop, and by surface friction at the substrate. In the scope of a thin drop approximation, we derive exact expressions for the flow in the drop that is generated by a given orientation profile. The flow has a natural decomposition into terms that depend entirely on the geometrical properties of the orientation profile, i.e. its bend and splay, and a term coupling the orientation to the shape of the drop. We find that asymmetric splay or bend generates a directed bulk flow and enables the drop to move, with maximal speeds achieved when the splay or bend is induced by a topological defect in the interior of the drop. In motile drops the direction and speed of self-propulsion is controlled by friction at the substrate.

Preprint: arXiv:1508.05242 [cond-mat.soft].

The Geometry of the Cholesteric Phase

Daniel A. Beller, Thomas Machon, Simon Čopar, Daniel M. Sussman, Gareth P. Alexander, Randall D. Kamien, and Ricardo A. Mosna, Phys. Rev. X 4, 031050 (2014). Open Access

We propose a construction of a cholesteric pitch axis for an arbitrary nematic director field as an eigenvalue problem. Our definition leads to a Frenet-Serret description of an orthonormal triad determined by this axis, the director, and the mutually perpendicular direction. With this tool we are able to compare defect structures in cholesterics, biaxial nematics, and smectics. Though they all have similar ground state manifolds, the defect structures are different and cannot be, in general, translated from one phase to the other.

Preprint: arXiv:1406.3304 [cond-mat.soft].

Knotted Defects in Nematic Liquid Crystals

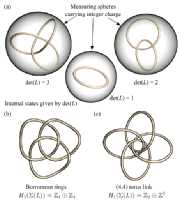
Thomas Machon and Gareth P. Alexander, Phys. Rev. Lett. 113, 027801 (2014).

We show that the number of distinct topological states associated to a given knotted defect, L, in a nematic liquid crystal is equal to the determinant of the link L. We give an interpretation of these states, demonstrate how they may be identified in experiments and describe the consequences for material behaviour and interactions between multiple knots. We show that stable knots can be created in a bulk cholesteric and illustrate the topology by classifying a simulated Hopf link. In addition we give a topological heuristic for the resolution of strand crossings in defect coarsening processes which allows us to distinguish topological classes of a given link and to make predictions about defect crossings in nematic liquid crystals.

Freely available at arXiv:1402.6898 [cond-mat.soft].

Threading Dynamics of Ring Polymers in a Gel

Davide Michieletto, Davide Marenduzzo, Enzo Orlandini, Gareth P. Alexander, and Matthew S. Turner, ACS Macro Letters 3, 255-259 (2014). Open Access

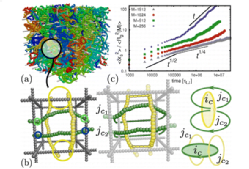
We perform large scale three-dimensional molecular dynamics simulations of unlinked and unknotted ring polymers diffusing through a background gel, here a three-dimensional cubic lattice. Taking advantage of this architecture, we propose a new method to unambiguously identify and quantify inter-ring threadings (penetrations) and to relate these to the dynamics of the ring polymers. We find that both the number and the persistence time of the threadings increase with the length of the chains, ultimately leading to a percolating network of inter-ring penetrations. We discuss the implications of these findings for the possible emergence of a topological jammed state of very long rings.

Freely available at arXiv:1306.4965 [cond-mat.soft].

Knots and Non-Orientable Surfaces in Chiral Nematics

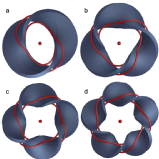
Thomas Machon and Gareth P. Alexander, Proc. Natl. Acad. Sci. USA 110, 14174-14179 (2013). Open Access

Knots and knotted fields enrich physical phenomena ranging from DNA and molecular chemistry to the vortices of fluid flows and textures of ordered media. Liquid crystals provide an ideal setting for exploring such topological phenomena through control of their characteristic defects. The use of colloids in generating defects and knotted configurations in liquid crystals has been demonstrated for spherical and toroidal particles and shows promise for the development of novel photonic devices. Extending this existing work, we describe the full topological implications of colloids representing non-orientable surfaces and use it to construct torus knots and links of type (p,2) around multiply-twisted Möbius strips.

Freely available at arXiv:1305.0143 [cond-mat.soft].

This work has been featured in a University of Warwick press release (prepared by Anna Blackaby) and also reported in several online science and technology websites. Now also highlighted in Liquid Crystals Today.

Preprints

Collaborators

I am lucky to have friends in many sunny and pleasant places around the world; Miha Ravnik (Ljubljana), Randy Kamien (Philadelphia), Mark Dennis (Bristol), Ray Goldstein and Adriana Pesci (Cambridge), Timon Idema (Delft), Andrea Liu (Philadelphia), Davide Marenduzzo (Edinburgh), Julia Yeomans (Oxford), Halim Kusumaatmaja (Durham).