Entropy

The second law of thermodynamics tells us systems will tend to increase their entropy over time. While this statement is well known even outside of physics, to make any sense of it one first needs to know what entropy is.

"Entropy is a measure of disorder" is the go-to sentence to give to someone unfamiliar with this slippery concept. Helpful as this loose definition often is, it is sometimes outright wrong and we are better served by returning to Boltzmann's equation:

Ignoring the constant and the logarithm, this says the entropy is essentially a count of the number of possible arrangements of a system . I.e., increasing entropy amounts to moving to a state that can be rearranged the largest number of ways without changing its macroscopic properties.

Configurational entropy

The simplest contribution to entropy comes simply from how many places you can find each particle. Each configuration of particle centres counts as 1 possible arrangement. Configurations of 4 spherical colloids in a box might look like:

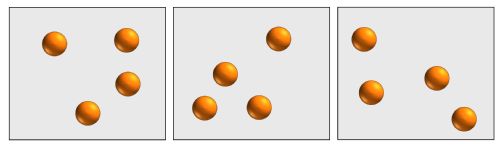
This configurational entropy increase with the number of particles and the volume available to them.

Conformational entropy

Flexible molecules, e.g. polymers, have an additional source of entropy from their conformation: For every position you can find them, they can adopt a large number of shapes and orientations. A few examples could be:

Importantly, the number of possible conformations depends on the local environment. Of particular importance, if a polymer is close to a hard surface, e.g. a wall or a colloid, then only those conformations that do not cross the surface are valid states and hence contribute to the entropy.

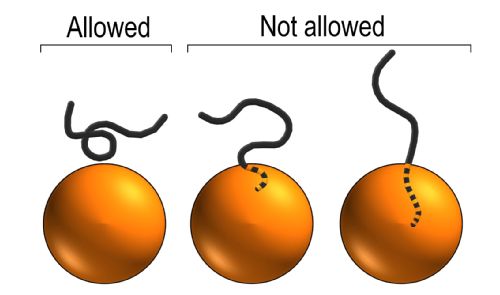
As a result the entropy is reduced when polymers are too close to a hard object, and consequently there is a region around the object which is depleted of polymers.

Competing entropies: depletion flocculation

The presence of hard objects in a polymer solution reduces the configurational entropy of the polymers by reducing the accessible volume, both from the objects themselves and the surrounding depletion region. Nothing can be done about the objects' actual volume, but the polymers stand to gain available volume if the depletion regions overlap.

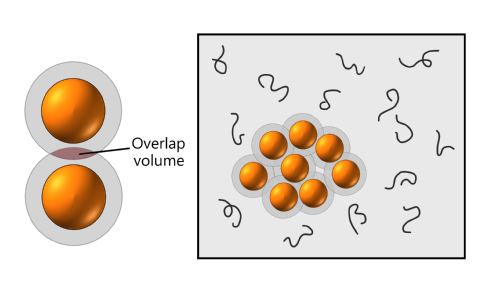
Thus polymers maximise their entropy if the hard objects cluster together. However, this also reduces the entropy of the hard objects, as only the relatively small number of arrangements in which they are all next to each other are allowed.

In practice, the additional conformational entropy of the polymers means they dominate, and the system separates into clusters (called 'flocs') and polymer-rich phases. This is aptly named depletion flocculation.