Parameter Inference and Interpretation

In order to estimate parameter values for our model we explored both Markov Chain Monte Carlo and Maximum Likelihood Estimation techniques. Here we present the results for the five parameter model as we believe it to be the most accurate.

Markov Chain Monte Carlo:

Parameter Data:

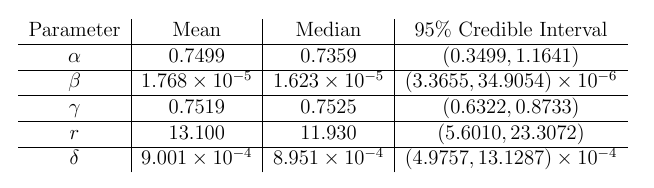
mcmcdat

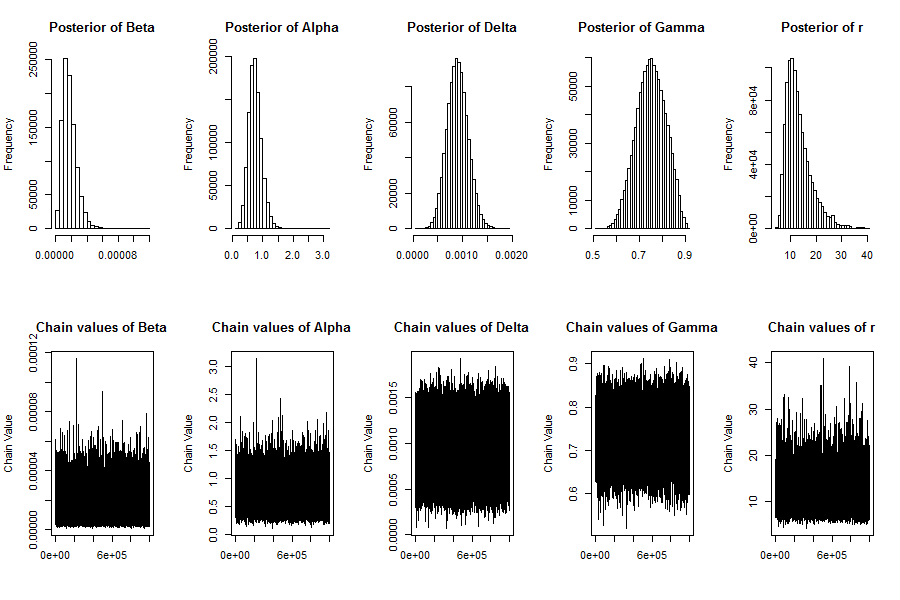
Histograms and Trace Plots:

mcmc5par

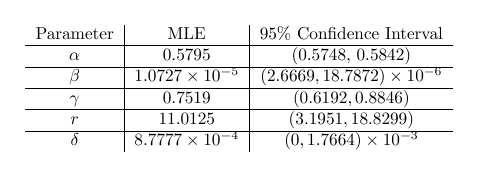
Maximum Likelihood Estimation:

Parameter Data:

mledat

Parameter Interpretation:

The $\alpha$ parameter:

In the model $\alpha$ fits as a geographical parameter in the spatial kernel: $K(d) = \exp(-\alpha d)$ this is used to weight the mixing component of the model to act heterogeneously.
As $K$ is an exponential function with range in (0,1) it is easy to measure the rate of decay:

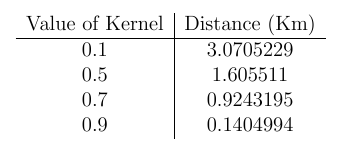
alphaint

The diameter of the Birmingham district we are working over is is 55km so the above data shows us the disease is very well localized spatially.

The $\delta$ parameter:

As stated in our model the probability a school i is infected at time t is given by $P_i(t)= 1- \exp(-\lambda_i^{\text{mixing}}(t))exp(-N_i\delta)$ This form allows us to study the effects of $\delta$ on the model as the probabilities factor implying independence. As smaller $exp( -N_i\delta)$ implies a greater chance of infection. We can then plot this drop off as a function of school size:
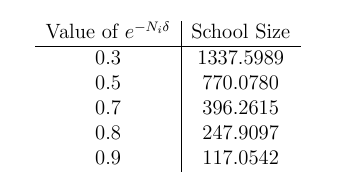
deltaint
As the average school size in Birmingham is 227.5 we can attribute between 80% to 90% of infections occurring due to school mixing as oppose to external pressure.

The $\gamma$ and $r$ parameter:

As these parameters are used in a negative binomial they are fairly easy to interpret.
Mean time is school is infectious: 4.3225 Weeks
Standard deviation: 2.3976 Weeks
As the time scale is of 9 weeks this shows us that once a school gets infected it generally stays that way for the majority of the epidemic.

Simulation and Public Policy