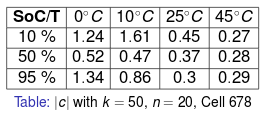
The Mathematical Nature of the Problem
Both subspace methods and neural networks have shown that adding a hidden variable leads to a better fit of data. In particular, we can observe that the hidden variable behaves really differently for different parameters. The plots below compare the hidden state with input and output, for 50% SoC and 25°C (above) and for 10% SoC and 0°C (below), obtained from neural network methods.
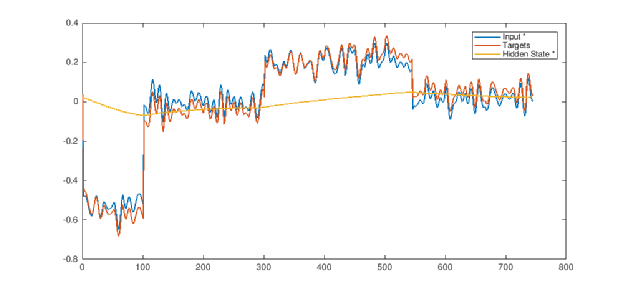
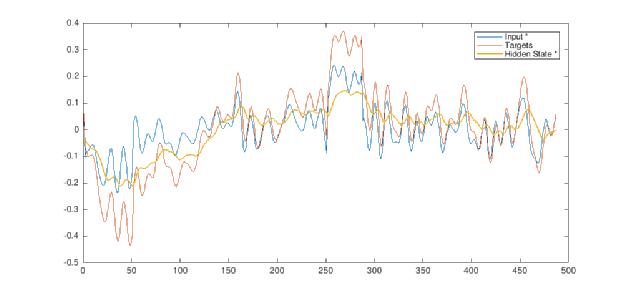
These considerations suggest a connection between the hidden variable and the over-potential. Indeed, we can see for high temperatures and SoCs that the hidden variable is low and the non-linearity redundant, leading to the unnecessary cost of a non-linear optimisation. These considerations are consistent with the Butler-Volmer equation: in the limiting case of low over-potential, the over-potential is linearly proportional to the current. On the other hand, for low SoCs and temperatures the hidden variable is better approximated by non-linear functions, in accordance with the Tafel relation. Subspace methods and neural networks also show an inverse proportionality between temperature and the multiplicative parameters and
, which appear in both the methods (for non-linear neural networks it corresponds to
and
).