Mathematics of Batteries
This is the webpage of the MA916 module done in the academic year 2016/2017 within the scope of MASDOC. The three authors of the page and the subsequent content are Letizia Angeli, Philip Herbert and Quirin Vogel. The project was supervised by Matteo Icardi and Bjorn Stinner, whom we would like to thank for their continuous support and valuable advice. MASDOC is funded by the EPSRC and we would like to extend our gratitude towards them.
The Objective
In this project, the aim was to find a method which was able to predict the outgoing voltage of a car battery given an input signal
, the temperature and the state of charge of the battery. Below we include a graph of the fit based on the paper [WBC+16]
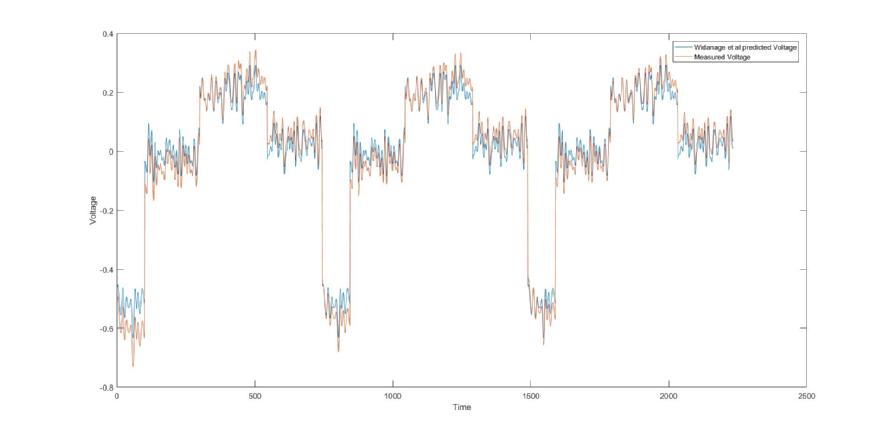
The ansatz was to apply the theory of linear dynamical system, i.e. use linear least squares (after smoothing) to compute the transfer function of a second order model (see [Lju99]) and then use a non-linear equation correction, based on electrochemical kinetics. For more details see Non-Linear Methods.
The Methods
In the theory of system identification there are various techniques to find a function relating the input (and a set of additional parameters) to the output. The most basic one is the theory of transfer functions leading to the theory (non-)linear least squares and minimisation problems. In this work, this method was applied with varying non-linear functions and solvers. For more details see Non-Linear Methods.
The subspace method is a different approach to predict the output of a system. It works by introducing an additional variable which represent the "internal state" of the system, see[Lju99]. Then, using the method of projecting onto a subspace, a method from linear algebra, a recursive system of equation is being solved.
The last method employed in the project are the so called neural networks. This promising method tries to imitate the way the human brain works; it consists of simulating lots of neurons which are weighting different input data and forwarding an output signal, then many of these neurons are connected in series and interact. Delays and hidden layers are some additional features.
The Findings
Several observations were made throughout the report. Overall, it can be said that all different approaches resulted in a tighter fit to the data than the original method. However, the tightness of the fit depends on the temperature and the state of charge. The most accurate method are neural networks, but, from a point of view of applications, subspace methods seem the most promising.
The subspace methods and the neural networks suggest that, basically, the problem is not time-dependent, meaning that the error decreases only slightly when one is taking into account the past values to predict the outcoming value. This could because the input signal professes a high degree of regularity, alternating between charging and discharging the battery, where both of these actions are performed with the same intensity. Thus, whilst applying the input current, not the temperature nor the state of charge change much overall. However, they also show the relevance of a hidden variable. This can be interpreted as the overpotential of the battery. The results obtained using all the three methods are consistent with the mathematical description of the batteries. In particular, the considered non-linear methods confirm that the non-linear correction is necessary for certain temperatures/state of charges. However, for certain temperatures, this does not improve the error. Our findings thus suggest that only at certain temperatures or state of charge this modification should be applied.
References
[Lju99] L. Ljung. System Identication: Theory for the User. Prentice
Hall information and system sciences series. Prentice Hall PTR,
1999.
[WBC+16] WD Widanage, Anup Barai, GH Chouchelamane, Kotub Uddin,
A McGordon, James Marco, and P Jennings. Design and use of
multisine signals for li-ion battery equivalent circuit modelling.
part 2: Model estimation. Journal of Power Sources, 324:61{69,
2016.


