Non-Linear Approximation Methods

Physical Background

The Butler-Volmer equation describes the electrochemical kinetics which occur inside a cell with both anode and cathode. In this model, we can assume that the over-potential is sufficiently large and thus the Butler-Volmer equation simplifies to the Tafel relation. The Tafel relation can be describe as follows: Let η be the over potential and let $i_d$ be the current density. For a and a constants (the so called Tafel constants) we have the following relation

$\eta=a+b\log(i_d)\, .$

Below we include a graph of the these relation affect the density

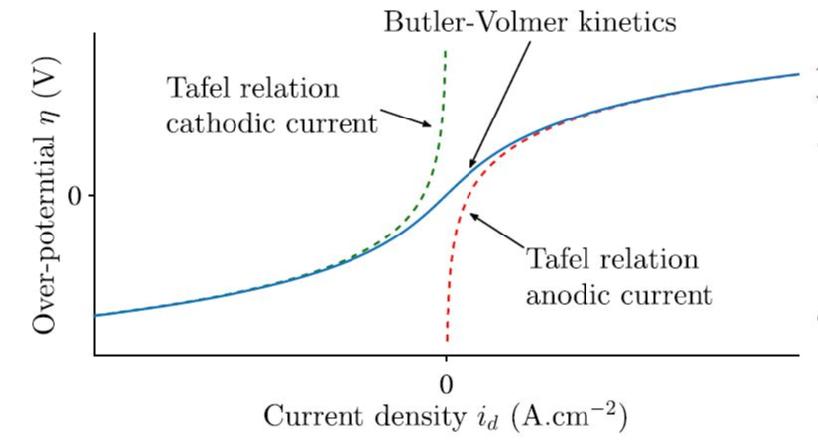
Tafel relation

When it thus comes to fitting the data, we need to take this non-linearity into account. We see that locally around the origin, the graph is linear whereas later the over potential of the Tafel relation approximates the true density, in a sigmoid like shape.

Modelling the Relation

Here, a two parameter approximation was chosen to model this non-linear behaviour

$\text{sig}(x)=c_1x/\sqrt{1+c_2x^2}\, .$

If we now compare the $L^2$ error using the non-linear correction to the strictly linear modole (see figure below) we notice for some temperatures, using a strictly linear model will lead to better results (dots below zero) than including the non-linear correction

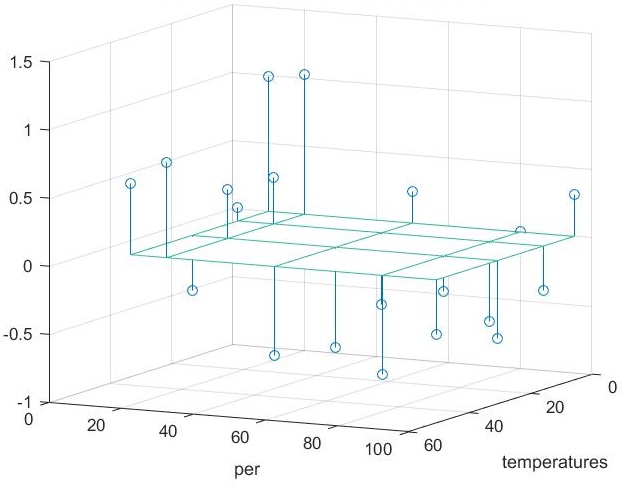
Linear Model vs Non-Linear one

Sensitivity Analysis

As it turns out, the performance of the standard Levenberg-Marquard fitting heavily depends on the initial values chosen for the parameters. If we start from Widanalage's data, and expand the $L^2$ values for the non-linear parameters around these parameters, we get a heavily fluctuating behaviour, as seen below

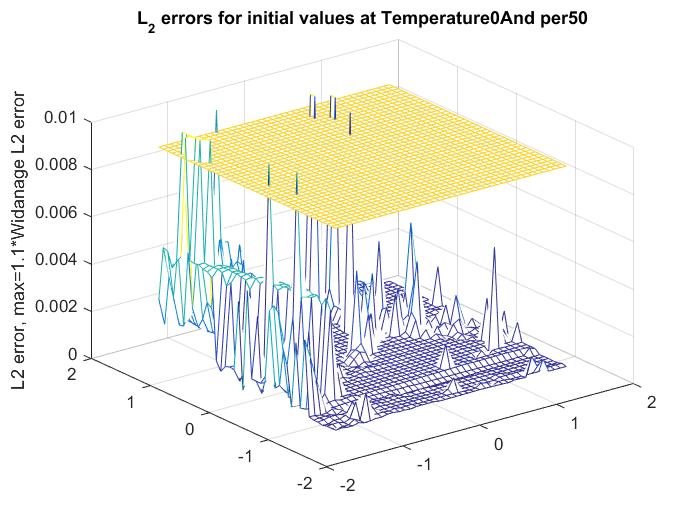
The chaotic behaviour of the data

The yellow plane represents the error achieved by Widanalage's method. To find stable initial values remains a challenge.