Subspace Methods

Subspace methods start with the assumption that our system taking input $i$ and output $u$ in continuous time is given by

$\begin{aligned}\dot{\underline{x}} (t) &= A \, \underline{x}(t) + \underline{b} \, i(t), \\ \dot{u}(t) &= \underline{c}^T \underline{x}(t) + d \, i(t),\end{aligned}$

with state vector $\underline{x}\in \mathbb{R}^p$ , state matrix $A \in \mathbb{R}^{p\times p}$ , input vector $\underline{b}\in \mathbb{R}^p$ , output vector $\underline{c}\in \mathbb{R}^p$ and direct feedthrough $d\in \mathbb{R}$ .

Throughout this project, we only considered the scalar subspace which simplifies some of the calculations to not be minimising in order to find a matrix, but simply a division of numbers.

We are not working in continuous time, so one can consider the discrete analogue

$\begin{aligned}\underline{x} (k+1) &= A \, \underline{x}(k) + \underline{b} \, i(k),\\u(k) &= \underline{c}^T \underline{x}(k) + d \, i(k).\end{aligned}$

Since only the input and output are known, one must work to construct such quantities, certainly they need not be unique, this is where the computation effort comes in.

For the live update, this method is somewhat changed for the reconstruction and relies on the ODE structure introduced earlier, but this method works for the Fourier method.

The method which is used to determine $A, \underline{b}, \underline{c}$ and $d$ starts by writing the equation in matrix form,
$\begin{pmatrix}u(0)\\u(1)\\\vdots\\u(k-1)\end{pmatrix}=\begin{pmatrix}\underline{c}^T\\\underline{c}^T A\\\vdots\\\underline{c}^T A^{k-1}\end{pmatrix}\underline{x}(0)+\begin{pmatrix}&d &0 &0 &\dots &0\\ &\underline{c}^T\underline{b} &d &0 &\dots &0\\ &\underline{c}^T A \,\underline{b} & \underline{c}^T \underline{b} &d &\dots &0\\ &\vdots&\vdots &\vdots & &\vdots\\ &\underline{c}^T A^{k-2}\,\underline{b} & \underline{c}^T A^{k-3}\,\underline{b}&\underline{c}^TA^{k-4}\,\underline{b} &\dots &d\end{pmatrix}\begin{pmatrix}i(0)\\i(1)\\\vdots\\i(k-1)\end{pmatrix},$

where we write

$\underline{u} = Q_{Bk}\, \underline{x}(0) + \mathcal{T}_k \,\underline{i}.$

Then one works to find these two matrices.

Two approaches were taken, a fourier method which dealt with all the data at once, and a method which looked back at a previous number of results, this second method is significantly more applicable.

It was hoped that the Fourier method would also, with the subspace tell us some information about the battery, which to some extent it does, through somewhat of a corrolation with the $c$ and $d$ values, which can be found in the appendix to the report.

This is the graphs from the 3rd peridod of the same dataset ( $\text{Cell} 678, \text{SoC} 10\%, $25^\circ\text{C}$ ), with the first one using mean zero data with the Fourier method and the second one using the local method.

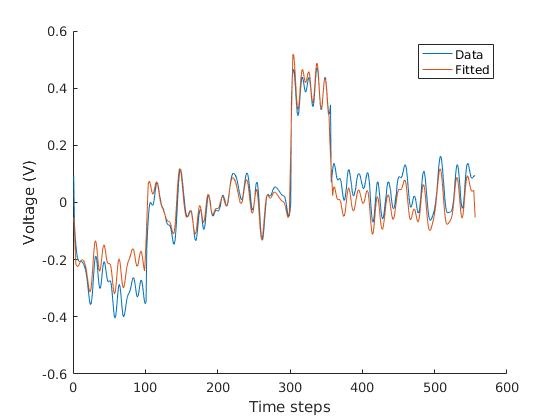
Cell 678, Soc 10%, Temp 25 degrees

The local method is less efficient than the fourier method (with a sysem being solved at each timestep), however it is more applicable and is still rather quick.