Authors: Matthew Egginton, Jamie Lukins and Jack Skipper
Supervisors: Timothy Sullivan, Florian Theil

---

Of critical importance in engineering, or any industrial application, is the consideration of data analysis, in particular that of smoothing noisy data and of analysing relationships between variables.

The former is a manifestation of the fact that any measurement taken of a physical setting will have some noise associated to it, essentially due to the fact that in taking a measurement, one disrupts the system one is trying to measure. This can occur throughout applied sciences as one tries to understand the actual state of a system while any data of that system will have associated noise of varying degree and type.

The latter comes from a black box type scenario, an unknown function, where one has input and output data from this system with errors attached to both, coming from inaccuracies in measurements and errors in models, and the goal is to recreate the black box.

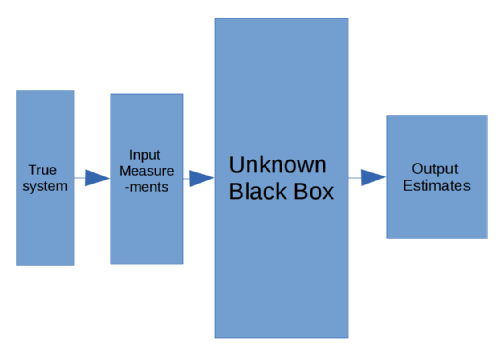
This problem can be seen to be in two parts:

• An inverse problem where there is input and output data with noise from a black-box and finding or approximating the black-box is the task.
• This is to recreate the black-box object and possibly improve so that with new input data the output data can be recreated in real time or faster.

We are motivated to understand this problem by a specific case brought to us by an industrial client. The client provided us with the input and output data pertaining to a car engine and vehicular emissions.

Mathematical Framework

We formulate the above problem mathematically and then discuss techniques to reverse engineer the process that the black box performs. In our formulation, we consider the problem from an entirely mathematical viewpoint without regard of the physical system. Our techniques should then be general enough to be applied in many industrial applications. We will further discuss the merits and pitfulls of each approach we consider.

A naive approach that we considered is a of linear interpolation of the data. This method is affected highly by noise in the data, as such it is not very successful in our application.

A more sophisticated technique is a Least Squares minimisation. This is where we try to fit a function to the data in such a way to minimise the noise in the data.

In a Bayesian approach to the problem, we consider the black box function to be a random function in some function space. Then a Markov Chain Monte Carlo algorithm can be run to draw a candidate for the black box function from a posterior distribution.

The Kalman Filter, is a real time process that we use in conjunction with the above to predict the outputs of the black box given that we have observed data. This has the benefit that it smooths out the noise in the outputs so that we are predicting outputs close to the true state of the system.

We implement the techniques discussed with our specific example from the automotive industry.

Here is an example of the results we have obtained.

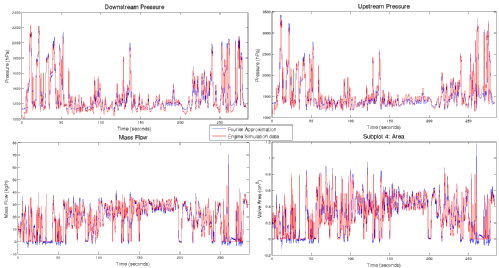
This is the least squares minimisation with a Fourier basis.

Acknowledgements

We acknowledge and thank the help of our supervisors Dr Tim Sullivan and Dr Florian Theil.
We also acknowledge the funding body EPSRC and the support from MASDOC CDT.

Contact: m.egginton at warwick.ac.uk, j.lukins at warwick.ac.uk jack.skipper at warwick.ac.uk