Engineering Application
Over recent history, there has been a trend for more restrictive emissions from internal combustion engines in motor vehicles. This reduction on emissions has caused companies within the motor industry to look at ways of altering and controlling the air flow through the engine.
E.G.R. System
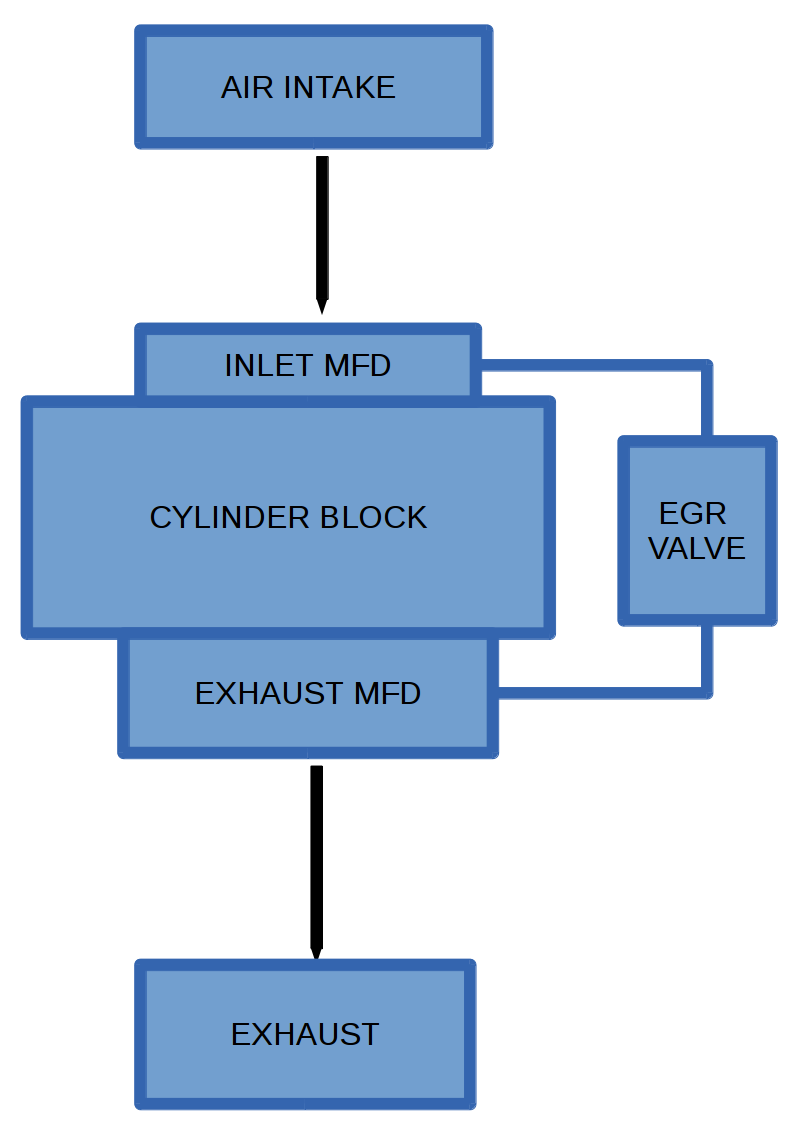
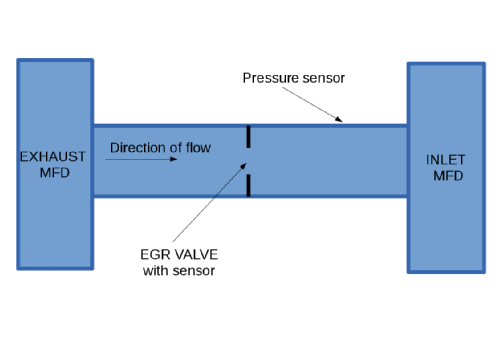
One problem that our client faces is the exhaust gas recirculation (EGR) flow, which is one such method used for controlling emissions. Of critical importance in this system is finding accurate values of the effective area of the valve in the system and the mass flow back around the engine through this system. These are related by a non-linear equation, the orifice equation:
which combines the upstream and downstream pressure.
Industrial Application
Within the engine, there is an electronic control unit (E.C.U.) which controls the area of the E.G.R. valve in order to regulate the mass flow. This is an important task, since recirculated flow will contain less oxygen for combustion but enough needs to be recirculated to comply with the government legislation. The E.C.U. produces outputs calculated from input data in an unknown way.
In this context, our client wishes to understand the mechanism used in the E.C.U. so as to estimate these measurements.
The aim would be, given the input time series of the data of pressures downstream and upstream of the valves, mass flow through the valve and area of the valve together with the corresponding outputs
, to construct the function
for suitable closed and bounded intervals
of
, that describes the black box procedure. That is, to find the function that attempts to take the input value
and map it to the true state of the system
. This is a problem in reverse engineering. The data we have been supplied with has
entries.
The data is analysis in detail here.
