Instantons and centres
We call an instanton any shift of the stationary solution of the deterministic Allen-Cahn $\bar{m}(x):=\tanh(x-x_0)$. The centre of the instanton $\bar{m}$ is then $x_0$, which we often refer to as the point of criticality.
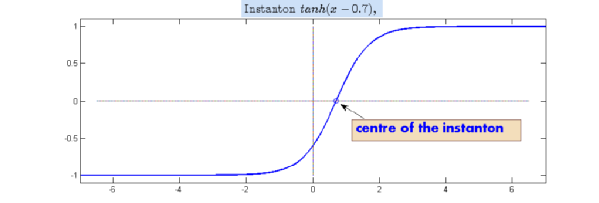
The above definition of centre of an instanton is generalised to arbitrary functions $p\in C^0(\mathbb{R})$. We say that such a $p$ has a centre $x_0$ if
$\displaystyle \int [p(x) - \bar{m}_{x_0}(x)]\bar{m}_{x_0}' \, \mathrm{d}x = 0$,
where $\bar{m}_{x_0}(x) = \tanh(x-x_0)$.
