Matthew King

I am no longer at University of Warwick and currently have a post doctoral fellowship at UCL in their Department of Medical Physics and Biomedical Engineering within the Biomedical Ultrasound Group, for an updated webpage please see here.Link opens in a new window

I have completed my forth year of MASDOC and third year of the PhD under the supervision of Dr. E. Brambley. Having sat my Viva at the start of January. My full thesis including corrections can be found hereLink opens in a new window.

I have since completed the David Crighton Fellowship at the University of Cambridge with Lorna Ayton, (3 months) continuing the work of my PhD. Since then I have started a research fellowship at UCL within the Biomedical Ultrasound Group under Bradley Treeby.

PhD Work:

During the PhD my work has focused on applying Complex analysis techniques in order to solve the pressure perturbation of the linearised Euler Equations. The work has application to the sound attenuation in ducts with acoustic liners such as those found in aircraft engines. My current work is in two areas, Studying the wave scattering of the Critical Layer by the Weiner-Hopf Technique. And extending the Modified-Myers (Brambley) Boundary Condition to account for a Quadratic Sheared flow profile, observing an effect of the critical layer, and a branch cut in the Dispersion relation. This continues work I have already completed, constructing analytic solutions to the Pridmore-Brown equation in a cylindrical duct, and understanding the contribution of the critical layer branch cut to the pressure perturbation under Fourier inversion. And in addition I have observed and tracked the modes for such a system, observing how and when the so-called hydrodynamic instability may be stabilised analytically, through its interaction with the Critical Layer branch cut.
Each of these works is summarised below.

In a 3D cylindrical duct that has a change of boundary conditions along the wall, considering a hard wall for $x less than zero$ and a lined wall for $x greater than zero$ . Iwas awarded the David Crighton FellowshipLink opens in a new window within DAMTP at the University of CambridgeLink opens in a new window to continue this work after my PhD alongside Dr. L. Ayton,Link opens in a new window coding the solutions in the Julia programming language to illustrate the results to a wider audience.
This considers the same profile as described above and constructs a Wiener-Hopf equation for the pressure perturbation. In doing so we can construct the wave field produced by a specific modal incoming wave.
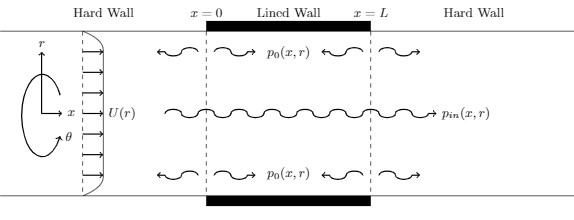
This work is also being expanded into a matrix Wiener-Hopf problem, ( $two$ ), considering two changes in the boundary condition where we consider a finite length region of lined wall along the length of the duct $zero less than x, x less than L$ , with hard walls either side $x less than zero, or, x greater than L$ .
See figures 2 and 3.
In both cases the aim is to construct the pressure perturbation analytically for any value of $x$ and incoming wave. This was done for an incoming wave that is modal and non modal, which have not been previously considered outside of this work. It is hoped that this work could be extended to comparisons between solutions to similar problems under mode matching procedures and experiments where specific wave modes can be excited.

For the remainder of my PhD the main focus of my work has been on studying the Modified-Myers boundary condition, under a quadratic shear flow. I have been able to formulate a closed form for the boundary condition under this flow profile, and we are able to observe not just the usual modes, but a branch cut in the complex wavenumber plane, considering exactly where the Critical Layer branch cut (or Continuous Spectrum) has previously been found for the full problems. We are once again able to observe the stabilisation of the Hydrodynamic Instability through the Critical Layer, and have been able to analytically continue the dispersion relation to allow us to locate the mode and derive it's contribution.

Over the first 3 years I have been constructing and understanding the properties of solutions to the Pridmore-Brown equation for an irrotational, inviscid, compressible, homentropic fluid flow through a lined 3D cylindrical duct. In particular have been constructing the greens function solution to the linearised Euler equations for the pressure perturbation for a point mass source. A parallel mean flow profile that follows that of a uniform flow across the centreline of a duct, and then is sheared following a quadratic profile within some boundary layer (not necessarily thin) is considered. See figure 1.
Solutions of the Pridmore-Brown equation are constructed using the Frobenius series, and must account for regular singularities, radii of convergence and branch cuts. The Green function solution given from this then undergoes Fourier inversion and complex analysis techniques are used to understand the effects of the various pole and branch cut contributions. These results can be compared to earlier works for other mean flows, and the differences understood.
This work has been published in the Journal of Fluid Dynamics: The critical layer in quadratic flow boundary layers over acoustic liningsLink opens in a new window

Work continues around this topic into the study of the Hydrodynamic instabilities. The Pridmore-Brown equation contains a regular singularity known as the Critical Layer which occurs as a branch cut in the Greens Function. It has been observed that the hydrodynamic instability, which typically dominates the far-field pressure and leads to a break down of the linearised Euler equations, be stabilised by moving through the Critical Layer branch cut, it's contribution in this case contained within integrating around the Critical Layer branch cut, which may be the dominant far-field contribution. This work has been presented as part of the 28t AIAA/CEAS Aeroacoustic Conference hosted by the University of Southampton. With a conference paperLink opens in a new window: Stabilisation of the Hydrodynamic Instability by the Critical LayerLink opens in a new window.
I have previously given a talk on this topic as part of the Waves in Complex Continua (Wavinar) Series in March 2022 with a recording found hereLink opens in a new window.

Teaching:

Over the course of the PhD so far I have completed two years of first year supervisions.
I have worked with first year students, both maths and non-maths (with mathematics modules) having three groups at a time. Over the academic year the supervisions involve an hour per group per week of support, face to face (2019-2020) and online (2020-2021), with planned content assuring key content was understood, and course work assignments could be completed to a suitable standard.
This course work was marked by myself and feedback was given to each student as individuals and within their groups.
Modules covered include (but not limited to):
MA106 Linear Algebra
MA131Link opens in a new window Analysis 1 & 2
MA133Link opens in a new window Differential Equations
MA134 Geometry and Motion
MA137 Mathematical Analysis

Prior to coming to the University of Warwick during the final year of my MMath at the University of Sussex I was involved with the student support centre and was given a 1:1 student in their final year of a BSc in mathematics.
In this role I was required to attend all of their lectures, some of which included new material for myself, take full and comprehensive notes, and then be able to relay and support in the understanding of all covered content.
Modules covered include:
G1100 Probability Theory
G1101 Random Processes
G1155 Coding Theory
G5106 Introduction to Mathematical Biology
G5126 Dynamical Systems

Prior areas of study:

During the first year of MASDOC as a part of the course I have worked alongside three of my colleagues on a group research project on the topic of Summation by Parts. This is a finite difference scheme for the numerical approximation of derivatives. In this project we looked at two different approaches for construction of these schemes; a brute force linear algebra method, and an approach making use of interpolating basis functions. The latter did not have much literature and we made clear sufficient conditions for attainment of specific degrees of accuracy among other result.

Prior to coming to Warwick I have studied an MMath degree at the University of Sussex. Here I focused on the analysis of Differential Equations and completed a masters project under the title ‘Analysis of Delay Differential Equations and their Application in Population Dynamics.’ This was supervised by Dr Yuliya Kyrychko. This looked at some of the basics behind steady state behaviour of delay differential equations with constant time delays, $\frac{dX}{dt}(t)=X(t, t-\tau)$ . This was observed in the setting of population growth models, and then observed further application to models for the spread of the Zika Virus.

Below: Figure 1: Illustration of a lined cylindrical duct containing a mean flow that is uniform about the centre line and the sheared within a radius h quadratically.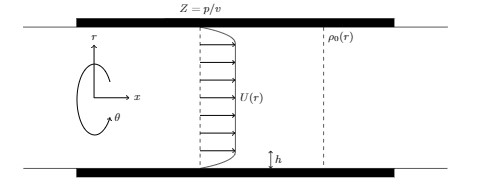 Image of Flow profile considered across my work Below: Figure 2: Illustration of a duct that goes from being hard walled to being lined with an incoming sound source and scattered waves from the change in boundary condition.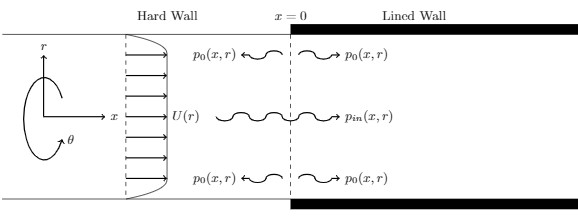 Scalar Wiener-Hopf Problem Schematic
Below: Figure 3: As above but for a finite length lined section leading to a matrix problem. Matrix Weiner-Hopf Schematic