9 October 2020: Martin Lotz (Warwick) Concentration of Measure, Integral Geometry and Optimization

The emergence of curious threshold phenomena in sparse signal recovery and optimization has led to a renewed study of classical problems in geometric probability. Specifically, it has been observed that the probability of recovering a structured signal by solving an optimization problem with random constraints increases sharply from negligible to almost one as the number of constraints (representing, for example, measurements) moves past a certain threshold. An explanation of this phenomenon can be found using a combination of ideas from integral geometry / geometric probability and measure concentration. I will give an overview of some old and new developments in this direction, and discuss further applications, for example to the convergence analysis of randomized algorithms.

This talk is based on joint work with Dennis Amelunxen, Mike McCoy, Ivan Nourdin, Giovanni Peccati, and Joel Tropp.

16 October 2020: Minhyong Kim (Warwick) Recent progress on Diophantine Equations in Two Variables

Slides: Download here

The study of rational or integral solutions to polynomial equations f(x_1, x_2,.., x_n) in two variables is among the oldest subjects in mathematics. After a brief description of the history, we will review a few of the breakthroughs of the last few decades and some recent geometric approaches to describing sets of solutions when the number of variables is 2.

23 October 2020: James Sprittles (Warwick) Noisy Nanofluidics

30 October 2020: Hong Liu (Warwick) Sublinear expander, cycles and graph minors.

We will introduce three central notions in graph theory: cycles, graph minors and expanders. We then sample some remarkable results on these topics and discuss some recent developments on embedding problems for cycles and minors using expanders.

6 November 2020: Felix Schulze (Warwick) Applications of geometric flows through singularities

Geometric flows have had striking applications to Geometry and Topology, such as the proof of the 1/4-pinched sphere theorem by Brendle-Schoen and Perelman’s celebrated proof of the Poincaré and Geometrisation conjectures. Both these results rely on a refined understanding of smooth solutions, with the second one utilising a surgery procedure to avoid singularities. It has emerged in recent years that also weak solutions, both for Ricci Flow and Mean Curvature Flow, have powerful applications. After an introduction to the setup and some more classical results, I will describe some of these recent applications of weak solutions through singularities.

13 November 2020: Vedran Sohinger (Warwick) The nonlinear Schrödinger equation, Gibbs measures, and many-body quantum mechanics

20 November 2020: William Parnell (Manchester) Elastostatic cloaking, low frequency elastic wave transparency and neutral inclusions

Cloaking of waves has been of interest for decades now although only in the last two decades have significant advances been made in achieving this in specific physical scenarios, including acoustics, electrodynamics and elastodynamics. The latter has proved significantly more difficult than the former two application areas and it transpires that a whole new theoretical framework (associated with so-called Willis coupling and equations) is required for invariance of the governing equations. In principle, an elastodynamic metamaterial cloak design should work at any frequency and for any wave type and it should conceal any object interior to it thus being independent of its nature and geometry, although in practice of course all of these properties are impossible. In this talk we take a step back and reconsider the theoretical underpinnings of elastostatic cloaking and the associated limit of low-frequency transparency from elastodynamics. We tie these concepts to that of the neutral inclusion (NI), which is a coated inclusion with the coating designed so as to render the inclusion invisible to a specific type of applied loading. The specificity of the loading and the dependence of coating on the inclusion properties is what makes the NI significantly different to ideal (currently unachievable) metamaterial design, although NIs do have the benefit of being more achievable to design and also of huge potential use in numerous materials science applications.

Neutral inclusions have long been known to be possible for hydrostatic loading, given that the governing equations reduce to scalar form in that scenario as for thermal and electrical problems. However for shear-type loading this is not the case and although “imperfect boundary conditions” (difficult to achieve in practice) can yield neutrality [1], it has been thought, even until recently that finite thickness coatings cannot ensure neutrality [2]. In [3] however, we addressed this problem, employing the impedance matrix approach to the two-dimensional equations of elastostatics in order to obtain conditions on coating properties in order that they act neutrally for both hydrostatic and in-plane shear loading. The coating is found to require anisotropic properties in general.

In this talk we summarise [3], provide links to elastodynamic cloaking and low-frequency transparency, noting in particular (and perhaps non-intuitively) that leading order low-frequency transparency is not equivalent to an elastostatic cloak in general. We introduce the concepts of weak and strong neutral inclusions to distinguish between these different concepts and show that the generalised self-consistent method from the theory of micromechanics [4] can be considered as introducing the concept of the weak (energetically neutral) neutral inclusion.

[1] Bertoldi, K., Bigoni, D. and Drugan, W.J., 2007. Structural interfaces in linear elasticity. Part II: Effective properties and neutrality. Journal of the Mechanics and Physics of Solids, 55(1), pp.35-63.

[2] Song, H.P., Song, K., Schiavone, P. and Gao, C.F., 2020. Design of a neutral elastic inhomogeneity via thermal expansion. Acta Meccanica, 231, pp. 2867-2876

[3] Norris, A.N. and Parnell, W.J., 2020. Static elastic cloaking, low-frequency elastic wave transparency and neutral inclusions. Proceedings of the Royal Society A, 476(2240), p.20190725.

[4] Christensen, R.M. and Lo, K.H., 1979. Solutions for effective shear properties in three phase sphere and cylinder models. Journal of the Mechanics and Physics of Solids, 27(4), pp.315-330.

27 November 2020: Ronald Solomon (Ohio State) Highlights from the Classification of the Finite Simple Groups

Slides: Download here

A first draft of the classification of the finite simple groups was completed in 2004 after decades of intense effort by scores of mathematicians. A project was initiated in 1981 by Daniel Gorenstein and Richard Lyons to produce a set of volumes giving a detailed proof of this classification theorem, resting on a small and explicit set of well-established background results. Lyons and I are continuing this project with the assistance of several collaborators, notably Inna Capdeboscq, Chris Parker and Gernot Stroth. Thus far, 8 volumes have been published by the A.M.S. and a 9th volume has been accepted for publication. A total of 12 volumes should complete the project. In this talk, I will described the logical structure of the entire proof and give some insight into how the final identification is accomplished for most of the finite simple groups.

4 December 2020: Thomas Gauthier (Ecole Polytechnique) Thick bifurcation loci in holomorphic dynamics​

In the family of quadratic complex polynomials $f_c(z)=z^2+c$, with $c\in\mathbb{C}$, the Mandelbrot set plays a central role. Indeed, one can for example see that its boundary is the bifurcation locus of the family, i.e. the locus where the dynamics of the polynomial changes drastically under small perturbations. In particular, the global understanding of this family of dynamical systems is intimately related to the geometry of the Mandelbrot set. One important question is to determine whether the boundary of the Mandelbrot set has positive area or not.

The aim of the talk is to explain that the equivalent problem in the family of all rational maps of a given degree, seen as holomorphic dynamical systems on the Riemann sphere, has a positive answer, to explain the tools involved in the solution of this problem, as well as why this strategy fails for the Mandelbrot set.

11 December 2020: Kathryn Lindsey (Boston College) Entropies of postcritically finite polynomials

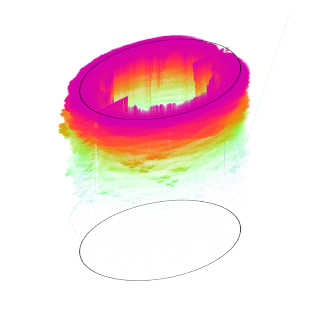The entropy of a dynamical system $f:X \to X$ is a nonnegative real number that describes how "chaotic" the system is. A polynomial $f:\mathbb{R} \to \mathbb{R}$ (or $f:\mathbb{C} \to \mathbb{C}$) is said to be postcritically finite (PCF) if the orbit under $f$ of every critical point forms a finite set. Which numbers arise as the entropies of PCF polynomials degree $d$? This is the "one-dimensional" analogue of a more famous open question: which real numbers arise as the dilatations of pseudo-Anosov surface diffeomorphisms of genus $g$? In both cases, a necessary condition is that the exponential of the entropy must be a special kind of number: a weak Perron number, i.e. a positive real algebraic integer that is $\geq$ the norm of all of its Galois conjugates. The Thurston Master Teapot (shown right) and Thurston Set associated to a family of such maps are 3- and 2-dimensional sets whose geometry encodes information about the set of weak Perron numbers realized as the exponential of entropies of maps in the family. These sets can also be thought of as analogues of the Mandelbrot set for families of iterated function systems. I will discuss Thurston Master Teapots and Thurston Sets and present some results and questions about them. This talk is based on joint work with Chenxi Wu, Diana Davis, and Harrison Bray.

15 January 2021: Henry Segerman (Oklahoma State) Raytracing and raymarching simulations of non-euclidean geometries​

I'll talk about two related projects, with two different groups, both aiming to see three-dimensional manifolds "from the inside". That is, we generate images assuming that light travels along geodesics in the geometry of the manifold. The first project, with Rémi Coulon, Sabetta Matsumoto, and Steve Trettel, uses ray-marching to generate the inside-view in all eight Thurston geometries. I'll explain the ray-marching technique, and some aspects of our implementation. The second project, with David Bachman, Matthias Goerner, and Saul Schleimer, visualizes "cohomology fractals" in hyperbolic three-manifolds. These images come from cohomology classes in the manifold, and are closely related to the sphere-filling curves discovered by Cannon and Thurston.

22 January 2021: Tim Sullivan (Warwick) Probability and Numerics: A Modern Retrospective​

Slides: Download here

The interplay of probability and numerical analysis is a topic with a long and interesting history, reaching back to Poincaré. In the computer age, probabilistic perspectives on numerical tasks such as linear algebra, quadrature, optimisation, and the solution of differential equations have enjoyed recurrent waves of interest and are now something of a "hot topic". This talk will give a general overview of the history of what now goes by the moniker of "probabilistic numerics", placing it in a modern context, including the often-overlooked contributions of A.V. Sul'din and F.M. Larkin. There will also be an indication of recent research results and future directions for the field, including applications to statistical inverse problems and scientific computing more generally.

29 January 2021: Agnese Barbensi (Oxford) Knotted Biopolymers

Many biopolymers - most notably DNA - are knotted, or present some entanglement phenomena. The geometry and topology of these biopolymers has profound effects on their functioning. Using tools coming from topology and knot theory can help understanding the relations between the spatial arrangement and the behaviour of these molecules. In this talk we will give a brief overview of some useful techniques and recent work in this area.

12 February 2021: Afonso Bandeira (ETH Zurich) Computational Hardness of Hypothesis Testing and Quiet Plantings

When faced with a data analysis, learning, or statistical inference problem, the amount and quality of data available fundamentally determines whether such tasks can be performed with certain levels of accuracy. With the growing size of datasets however, it is crucial not only that the underlying statistical task is possible, but also that is doable by means of efficient algorithms. In this talk we will discuss methods aiming to establish limits of when statistical tasks are possible with computationally efficient methods or when there is a fundamental "Statistical-to-Computational gap" in which an inference task is statistically possible but inherently computationally hard. We will focus on Hypothesis Testing and the "Low Degree Method" and also address hardness of certification via "quiet plantings". Guiding examples will include Sparse PCA, bounds on the Sherrington Kirkpatrick Hamiltonian, and lower bounds on Chromatic Numbers of random graphs.

19 February 2021: Rachel Newton (Reading) Diophantine equations and when to quit trying to solve them

The study of integer or rational solutions to polynomial equations with integer coefficients is one of the oldest areas of mathematics and remains a very active field of research. The most basic question we can ask about such an equation is whether its set of rational solutions is empty or not. This turns out to be a very hard question! I will discuss modern methods for proving that the set of rational solutions is empty, as well as their limitations. Along the way, I will describe some recent work with Martin Bright concerning the wild part of the Brauer-Manin obstruction.

26 February 2021: Lisa Carbone (Rutgers) A Lie group analog for the monster Lie algebra

Slides: Download here

The monster Lie algebra is an infinite dimensional Lie algebra constructed by Borcherds as part of his program to solve the Conway-Norton conjecture about the representation theory of the Monster finite simple group M. We describe a construction of a Lie group analog for the monster Lie algebra and its relationship with the Monster finite simple group.

5 March 2021: Mario Bonk (UCLA) Fractals and the dynamics of Thurston maps

A Thurston map is a branched covering map on a topological 2-sphere for which the forward orbit of each critical point under iteration is finite. Each such map gives rise to a fractal geometry on its underlying 2-sphere. The study of these maps and their associated fractal structures links diverse areas of mathematics such as dynamical systems, classical conformal analysis, hyperbolic geometry, Teichmüller theory, and analysis on metric spaces. In my talk I will report on some recent developments and open problems in this area.

12 March 2021: Linda Cummings (New Jersey) Dewetting and dielectrowetting in thin films of nematic liquid crystals

Thin films of nematic liquid crystal (NLC) find widespread industrial use, in applications ranging from liquid crystal display devices to liquid lenses and optical shutters. Understanding how such films spread and flow is therefore important from an industrial perspective as well as being of fundamental scienti c interest. We will describe how asymptotic methods (lubrication theory) can be applied to derive a simplified model for the free surface evolution of NLC films in a number of different settings. Of particular importance for film behavior is the orientation of the NLC molecules, both within the bulk film and at interfaces. The former is dictated by elastic effects and by the presence of applied external fields such as an electric field; while the latter depends primarily on interactions of the NLC with the adjacent material (a phenomenon known as anchoring). We will present simulations of our model that illustrate film behavior both without (dewetting) and with (dielectrowetting) an applied electric field, showing good qualitative agreement with available experimental data.

19 March 2021: Jennifer Balakrishnan (Boston University) Rational points on curves and quadratic Chabauty

Slides: Download here

Let C be a smooth projective curve defined over the rational numbers with genus at least 2. It was conjectured by Mordell in 1922 and proved by Faltings in 1983 that C has finitely many rational points. However, Faltings' proof does not give an algorithm for finding these points, and in practice, given a curve, provably finding its set of rational points can be quite difficult.

In the case when the Mordell--Weil rank of the Jacobian of C is less than the genus, the Chabauty--Coleman method can be used to find rational points, using the construction of certain p-adic line integrals. Nevertheless, the situation in higher rank is still rather mysterious. I will describe the quadratic Chabauty method (developed in joint work with N. Dogra, S. Müller, J. Tuitman, and J. Vonk), which can apply when the rank is equal to the genus. I will also highlight some examples of interest, from the time of Diophantus to the present day.

30 April 2021: Benedikt Loewe (Cambridge) Analysis in non-Archimedean fields

The real numbers are up to isomorphism the only completely ordered field with a countable dense subset. We consider non-Archimedean ordered fields whose smallest dense subset has cardinality kappa and investigate whether anything resembling ordinary analysis works on these fields.

In particular, we look at generalisations of the intermediate value theorem and the Bolzano-Weierstrass theorem, and realise that there is some mathematical tension between these theorems: the intermediate value theorem requires some saturation whereas Bolzano-Weierstrass fails if the field is saturated. We consider weakenings of Bolzano-Weierstrass compatible with saturation and realise that these are equivalent to the weak compactness of kappa.

This is joint work with Merlin Carl, Lorenzo Galeotti, and Aymane Hanafi.

7 May 2021: Gunnar Carlsson (Stanford) Topological Deep Learning

Machine learning using neural networks is a very powerful methodology which has demonstrated utility in many different situations. In this talk I will show how work in the mathematical discipline called topological data analysis can be used to (1) lessen the amount of data needed in order to be able to learn and (2) make the computations more transparent. We will work primarily with image and video data.

14 May 2021: Elise Goujard (Bordeaux) Geometry of large genus flat surfaces

Gluing the opposite sides of a square give a flat torus: a torus endowed with a flat metric induced by the Euclidean metric on the square. Similarly, one can produce higher genus surfaces by gluing parallel sides of several squares. These "square-tiled surfaces" inherit from the squares a flat metric with conical singularities. In this talk we will present several recent results and conjectures on the large genus asymptotics of these surfaces, and more generally of some families of flat surfaces (joint work with V. Delecroix, P. Zograf and A. Zorich). We will also see how these results can be interpreted in the language of closed curves on surfaces and meanders.

21 May 2021: Matt Keeling (Warwick) COVID-19: Mathematical Modelling from Warwick

The COVID-19 has had a massive impact on health, wealth and society worldwide. There are a number of key questions where mathematics can play an influential role in terms of a rigorous understanding of the current situation (now-casting) and in terms of projecting dynamics into the short- and long-term. Researchers at Warwick have played a key role in providing advice that has fed into UK policy. In this talk I'll discuss five main findings: the basic model and early findings; short-term circuit breakers; vaccine predictions; optimal dynamics; and a look to the immediate future.

28 May 2021: Greg McShane (Fourier) Markoff numbers, algebra, combinatorics and geometry

Slides: Available here.

The Markoff numbers are those integers which appear in a solution $(x,y,z)$ over positive integers of the Markoff cubic \[x^2 + y^2 + z^2−3xyz = 0.\]