Electronic band structure

Energy-wavevector relationship

In a solid, the free electron approximation is no longer valid, so to describe the behaviour of the electrons we need to use another approach. The Schrödinger equation fully describes the behaviour of electrons, when an appropriate Hamiltonian is used.

$H|\psi\rangle = E | \psi \rangle$

A Hamiltonian that fully describes the system requires the inclusion of the interaction between electrons and ions, and is given by:

$H = \sum_{i} \frac{\vec{p}_i ^2}{2 m_e} + \sum_{j} \frac{\vec{p}_l ^2}{2 M_l} + \sum_{i.l} V ( \vec{r}_i - \vec{R}_l) + \sum_{l,m} U ( \vec{R}_l - \vec{R}_m) + \sum_{i,j} \frac{e^2}{4 \pi \epsilon_0} \frac{1}{| \vec{r}_i - \vec{r}_j|}$

Where $m_e$ is the electron mass $M_i$ is the ion mass and $\vec{R}$ is the separation between the ion and electron. Directly solving this Hamiltonian is very complex, so approximations are usually employed to simplify the task. Important approximations are the Born-Oppenheimer approximation[1] the one electron approximation[1] and the mean-field approximation[1]. The Born-Oppenheimer approximation states that the electrons react instantly to the motion of the ions, but the reaction of the ions is much slower, allowing us to ignore the motion of the ions. The one electron approximation assumes all electron-electron interactions are averaged, and the mean-field approximation states that all the electrons are in identical surroundings with regards to the ions and their equilibrium positions. These approximations allow us to use a simplified Hamiltonian:

$H = \frac{\vec{p}^2}{2 m_e} + V_0 (\vec{r})$

$V_0(\vec{r})$ represents the periodic potential in the lattice, utilising the translational symmetry that is present.

Parabolic approximation

By considering the electron energy dispersion only around the $\Gamma$ -point (centre of the Brillouin zone) we arrive at an equation for the parabolic approximation at the extrema of the conduction and valence bands (which are in general located at the $\Gamma$ -point for semiconductors). This can be shown to be:

$E_{\mathrm{e,h}}(\vec{k}) = E_{\mathrm{e,h}} (0) \pm \frac{\hbar ^2 \vec{k}^2}{2 m ^{*}}$

For large gap semiconductors this equation tends to hold well, but this proves to be ineffective for narrow gap semiconductors such as InN, because the interaction between conduction and valence bands cannot be ignored. In this case Kane's k.p perturbation theory[2] is used.

k.p perturbation theory

k.pperturbation uses the fact that the cell periodic functions for the electrons for any $\vec{k}$ form a complete set. The wave function used for this can be written as:

$\psi = u_{n\vec{k}} (\vec{r}) \exp(i \vec{k} \cdot\vec{r}) = \left[ \sum c_m U_{m\vec{k_0}} (r) \right] \exp (i \vec{k} \cdot \vec{r})$

Using $\psi$ in the Schrödinger equation, and the fact that the wave function for $\vec{k}  = \vec{k_0}$ in the n^thband is $\psi =\exp(i \vec{k_0}\cdot \vec{r}) U_{m \vec{k_0}} (\vec{r})$ should produce[3]:

$\left[ - \frac{\hbar^2}{2 m_0} \nabla^2 + \frac{\hbar}{m_0} \vec{k_0} \cdot \vec{p} + \frac{\hbar^2 k_0 ^2}{2 m_0} + V(\vec{r}) \right] U_{m \vec{k_0}} (r) = E_m (\vec{k_0}) U_{m \vec{k_0}} (\vec{r})$

Effective mass

The electron movement in a lattice is different from the movement in free space. In a crystal the electron will pass through energy band full of electrons and some with very few. Also we need to consider that the electron is subject to different forces, internal and external. The internal forces are due to the different particles within the crystal. Since it is difficult take into account all the internal forces instead of having $F_{total}=F_{ext}+F_{int}=ma$ we define a effective mass that takes in account the particle mass as well as the effects of the internal forces ( $F=m^*a$ ).

In order to describe the particle in the crystal we need to consider a wave packet and the uncertainty principle, which states we can measure the position and the momentum of the wave packet simultaneity with a precision of $\Delta x\Delta\hbar\approx\hbar$ . the group velocity od the wave packet is given by $v=\frac{d\omega}{dk}=\frac{1}{\hbar}\frac{d\epsilon}{dk}$ .

For a particle acted by a force $\vec{F}$ , for example, if we apply an electric field, we will have $d\epsilon=(\frac{d\epsilon}{dk})dk=vd(\hbar k)$ with $d(\hbar)$ the crystal momentum.

From Newton law we have $f/m^{*}=dv/dt$ and using the above expressions we will get

$\frac{F}{m^*}=\frac{1}{\hbar}\left(\frac{d^{2}\epsilon}{d\hbar^2}\right)\frac{dk}{dt} \Leftrightarrow$ $\hbar \frac{dk}{dt}\frac{1}{m^*}=\frac{1}{\hbar}\left(\frac{d^{2}\epsilon}{d\hbar^2}\right)\frac{dk}{dt}$

This will give an expression for the effective mass (1D):

$m^*=\frac{\hbar^2}{d^{2}\epsilon/dk^* }$

As we can see from the above expression the sign of the effective mass depends on the curvature of the band.

Bandgaps

The band gap is the energy difference between the lowest point of the conduction band ( conduction band edge) and the highest point of the valence band (valence band edge).

A semiconductor can have a direct band gap or a indirect band gap. A direct band gap is characterised by having the band edges aligned in k, so that a electron can transit from the valence band to the conduction band, with the emission of a photon, without changing considerably the momentum. On the other hand, in the indirect band gap the band edges are not aligned so the electron doesn't transit directly to the conduction band. In this process both a photon and a phonon are involved.

Si bandstructure

Energetic bands

The energetic levels in atoms and molecules can be discrete or can split into a near-continuum of levels called a band. The energy bands can be classified as empty, filled, mixed or fobidden bands. The energetic levels are occupied by the electrons (distributed according to Pauli exclusion principle) , starting with the lowest energy value level. The electrons that contribute to the electrical conduction occupy the higher energy bands. The valence band corresponds to the highest energy band that contains electrons. The valence band can be fully or partial occupied. The allowed (empty) states in the valence band add contribution to the electric current. The conduction band is the lowest energetic band with unoccupied states.

In materials the conducting bands of empty, filled or allowed states can interfere with forbidden bands, also called band gaps. The width of the band gap (width measured in energy units) determines the type of material: insulator, semiconductor, metal. If at temperatures in the range of room temperature the electrons in a pur semiconductor gain sufficient energy to overcome the energy of the bandgap E_g, the semiconductor is called intrinsic semiconductor.

Energy Band Gaps in Materials

Description of the electronic bands in solids[8].

Density of states

The density of states provides numerical information on the states availability at each energy level. A high value for the density of states represents a high number for the energetic states ready to be occupied. If there are no available states for occupation in an energetic level, the value for the density of states will be zero.

Density of states

Schematic diagram illustrating the representation of the electronic density of states depending on dimensionality[7].

Scanning tunneling microscope is an advanced type of computerized microscope that can probe the density of states of nanostructures. With a scanning tunneling microscope both empty and filled states can be probed in a single measurement. The electric current is measured as a function of the bias voltage and the cumputer program will plot a curve describing the conducting character of the nanostructure. The first derivative, dI/dV, is a first aproximation of the local density of states. The local density of states is a measure of the amount of filled or empty states present at a specific value of energy.

scanning tunneling spectroscopy

Example of scanning tunneling spectroscopy data[4].

Holes

Holes are fictious particles [5] considered positively charged with charge |e|, having positive effective mass m_h and energies $E=+\hbar^2*k^2/2m_h$ . These fictious particles "occupy" the empty states in the energetic bands. A hole is actually a missing electron in an energy band. The concept of holes as positively charged particles has been introduced in order to simplify the calculations for the electronic transitions in an almost fully occupied valence band.

Doping

The pure silicon, for example, is a poor conductor. In order to improve the conductivity properties, the concentration of charge carriers must be increased. This process is possible by introducing impurities in the silicon crystal. This method is called doping and give rise to additional number of electrons or holes in the semiconductor. The doped semiconductor is called extrinsic.

Depending on the impurities type, there are acceptor dopants (Gr. III elements) and donor dopants (Gr. V elements). This classification leads to p-type, respectively n-type semiconductors. Due to the doping process, the Fermi level, normally at the center of the band gap, will be shifted according to the type of semiconductor. In the p-type materials, there is a generation of extra number of holes. The energetic levels of the acceptor impurities will occupy the space right on the top of the valence band. The Fermi level, in this case, will be shifted towards the valence band. For the n-type materials, the number of electrons is increased and the donor impurity levels are situated right under the conduction band, which causes the Fermi level to be shifted towards the conduction band.

Illustration of intrinsic and extrinsic types of silicon semiconductor [6].

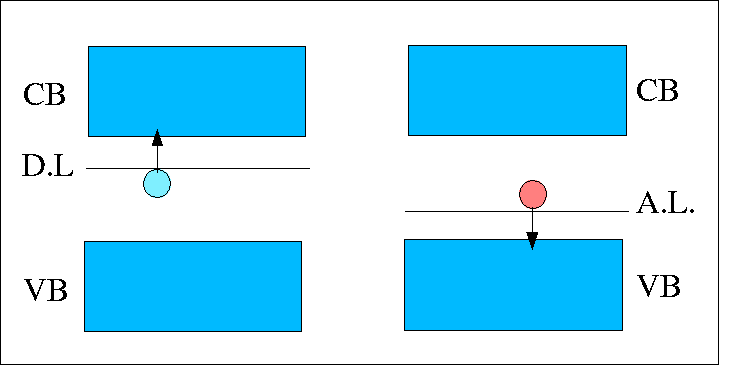
Acceptor-donor levels

Position of the donor level (D.L.) occupied with electrons, and, acceptor level (A.L.) of holes with respect to the conduction and valence band [7].

References

B. Ridley, Quantum Processors In Semiconductors, Oxford Science Publications, 1993.
E. O. Kane, J. Phys. Chem. Solids 1, 249 (1957).
B. Nag, Electron Transport In Compound Semiconductors, Springer-Verlag, 1980.
http://www.physics.berkeley.edu/research/crommie/research_stm.html
Hook, J.R. and Hall, H.E. Solid State Physics. 2nd ed. Chichester: John Wiley & Sons, 1991.
http://www.answers.com/topic/n-type-silicon-technology (with slight editing for better layout)
http://org.ntnu.no/solarcells/pages/pn-junction.php
http://www-opto.e-technik.uni-ulm.de/lehre/cs/
http://micro.magnet.fsu.edu/primer/java/lasers/diodelasers/index.html

Bibliography

John Singleton (2001). Band Theory and Electronic Properties of Solids Oxford Master Series in Condensed Matter Physics. ISBN 0-19-850644-9
K. Seeger(1991), SSemiconductor physics: an introduction. Springer-Verlag

Department of Physics

Electronic band structure

Energy-wavevector relationship

Parabolic approximation

k.p perturbation theory

Effective mass

Bandgaps

Energetic bands

Density of states

Holes

Doping

Links

References

Bibliography

See also