Properties:

      Reducing the radius of the cluster (assumed to be spherical) results in the blue shift of the characteristic transition energies such as excitons, and several examples are given in figure 1 taken from Ekimov (1991). He also makes several general points concerning such quantum confinement effects.  

 (1) As the radius R becomes very small, the energy levels for carriers change from continuous bands to a ladder of discrete levels.

 

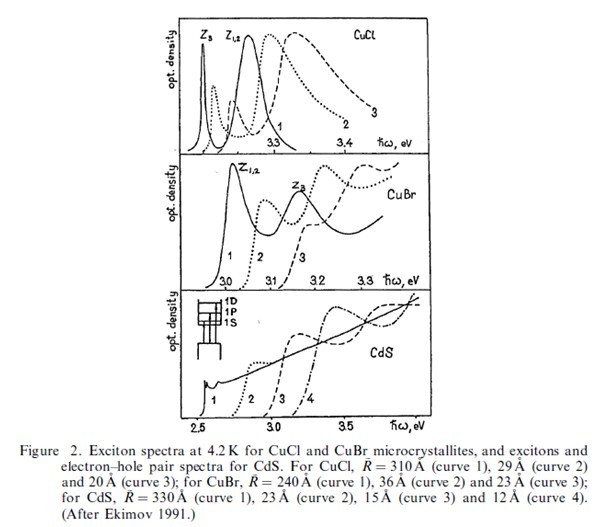
 (2) There is an enhanced volume-normalized oscillator strength of exciton features as R is reduced. This arises because the oscillator strength becomes concentrated over sharp electron¡Àhole transitions, rather than being distributed over a continuum of states as for the case of bulk semiconductors.

 (3) There is an enhanced exciton nonlinearity and a reduction in optical power required for optical saturation relative to the bulk semiconductor. Cooperation between quantum dots for optical nonlinear e. ects is also an important practical factor (for example Takagahara (1992)).

 (4) Most theoretical treatments assume spherical shapes for the crystallite, and this is a reasonable approximation in many cases (Goldstein et al. 1992).