Quantum Dots

The terms quantum dots (QDs), nanoclusters, artificial atoms and nano crystals are different terms used to describe metals or semiconductors in the size range between 1-100 nm. They gained a great deal of attention because of their outstanding properties and potential applications. QDs are the best candidate to fill the gap between atoms/molecules and bulk. Due to ultimate size reduction, carriers are confined in all three spatial directions. On other words, no more possible free propagation of carrier, which lead to discrete energy levels in a quantum dot resembling those of an atom. These systems may contain atoms up to few thousands.

As a result of the small size of QDs, the surface area is relatively very high, which increases midgap states and make the cluster reactive chemically. Thus, they may oxidize easily if they were exposed to air. Consequently,the quality of these dots reduces as their optical and electronic properties modifies.

To avoid these problems it is important to passivate the surface to satisfy its dangling bonds and terminate or at least reduce the number of midgap states. This can be achieved by passivating the surface using either organic or inorganic capping agent. The latter may have other advantages; as it prevent the cluster from further growth so it enhance the stability of QDs. Moreover, a good selection of the capping material could be useful in functionalizing the dots [1].

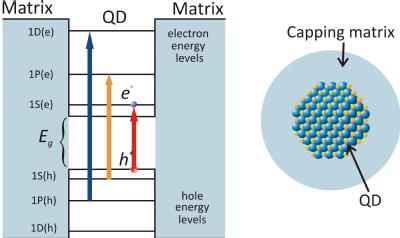
A schematic of a QD and its atomic like energy levels

QD size reduction is accompanied with an emission energy blue shift. This is can be modelled using the elementary particle in a box model [2] . Assuming that QD has a diameter R, the energy separation between the highest occupied energy level and the lowest unoccupied energy level E_g(QD) :

$E_g(QD)=E_{gbulk}+\frac{\hbar^2 \pi^2}{2m_{eh}R^2}$

where

$ m_{eh}= \frac{m_e m_h}{m_e+m_h}$

Growth of QDs

Properties of QDs

theoretical models of QDs

Experimental constraints for theoretical models

Reference

Moriarty P., Nanostructured materials, Reports on Progress in Physics, 64, (2001) 297-381
Klimov V., Nanocrystal Quantum dots: from fundamental phtophysics to multicolor lasing, Los Alamos Science, 28 (2003), 214-220
A. D. Yoffe. Low-dimensional systems: quantum size effects and electronic properties of semiconductor microcrystallites (zero-dimensional systems) and some quasi-two-dimensional systems [J]. Advances in Physics, 2002, Vol.52:799-890.