Dislocations 1: Phenomenology

A dislocation is the boundary between the portions of a material that are sheared with respect to each other. One type of dislocation is called screw dislocation as seen in figure

A screw dislocation.

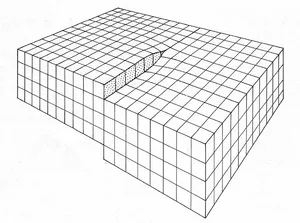
Another type of dislocation is a edge dislocation as in figure

An edge dislocation.

As one can see from figure

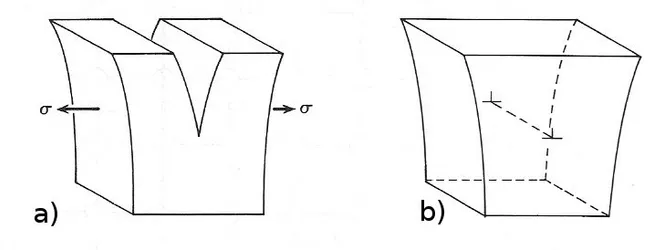
The dislocation line of an edge dislocation

the dislocation opens up from a line running through the material called a dislocation line. Dislocations are characterised by a so-called Burger’s vector $\textbf{b}$ . It is basically the difference vector between the lattice on one side of the dislocation and that of the other. Choose a loop surrounding a disc with unit normal vector xi such that the dislocation line punctures the disc as in figure

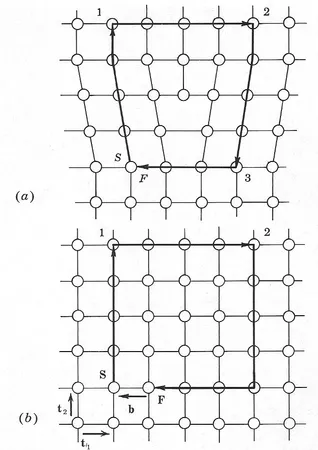
The loop with normal xi and Burger

In the figure above $\xi$ is pointing out of the plane and $\textbf{b}$ is pointing to the left. As one can see, edge dislocations have $\mathbf{b} \cdot \mathbf{\xi}=0$ while screw dislocations have $|\mathbf{b} \cdot \mathbf{\xi}|=|\mathbf{b}|$ . Often, dislocations have both screw and edge character, so one can decompose its Burger’s vector by $\mathbf{b}_{s}=\mathbf{b}\cdot \mathbf{\xi}$ and $\mathbf{b}_e = \mathbf{\xi} \times (\mathbf{b} \times \mathbf{\xi})$ Of course, one can decompose $\mathbf{b}$ into any combinations of vectors $\mathbf{b}_1$, $\mathbf{b}_2$ such that $\mathbf{b} = \mathbf{b}_1 + \mathbf{b}_2$ . This does physically occur in the manifestation of branching dislocation lines. See figure

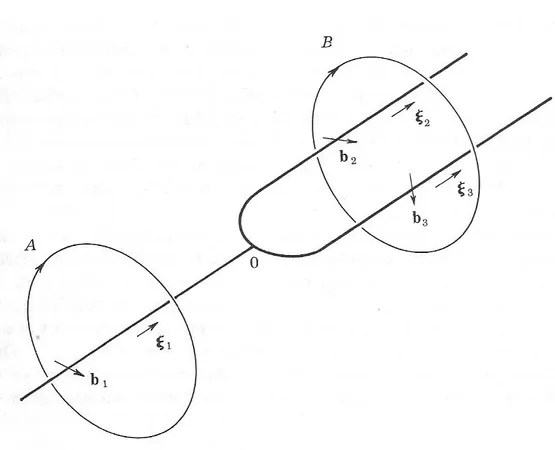
Equivalent Burger

Note that one can glide the loop with normal $\mathbf{\xi}_1$ to beyond the branching point without the loop intersecting the dislocation lines. As with any boundary, $\mathbf{\xi}_1$ has an orientation (sign). If one defines the sign with respect to the branching point with positive in one direction and negative in the other, the sign of the Burger's vector should change accordingly and $\sum_i \mathbf{b}_1=0$ . Hence dislocations are conserved and continuous so they need to end in another dislocation, at a surface or on an impurity. Dislocation lines are often shaped like a flat U-shape ending at a surface. Dislocation lines not lying on a misfit bit merely connecting the misfit dislocation with a surface is called a threading dislocation. The next figure depicts a typical situation with a dislocation changing from a misfit to a threading character.

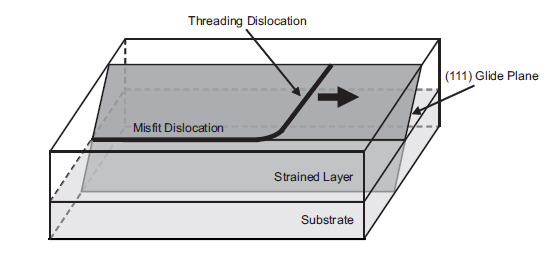
Threading Dislocation

Some form closed circuits and there are several ways how they can be formed. One of them is by growing another layer on top of such a U-shaped dislocation line ending at the top surface. The ends of a dislocation on a surface is the start of a new dislocation in the new layer. During the deposition of the new layer, the ends may move closer together until they meet, forming a loop. Dislocation lines can move during or after growth. They may "glide" or move up, very much like opening a zipper.