An ellipsometer enables the measurement of the thickness of semi-transparent films. The instrument relies on the fact that the reflection at a dielectric interface depends on the polarization of light while the transmission of light through a transparent layer changes the phase of the incoming wave depending on the refractive index of the material [1].

A typical multispectroscopic ellipsometer that emits light of wavelengths 250-800 nm from a xenon bulb at 10nm intervals, can be used to measure the thickness of thin films. This light passes through a monochromator and makes contact with the sample at a 70˚ angle of incidence. The reflected light is measured, and with the use of the Cauchy Absorbent Dispersion Formula various properties, including sample thickness, are derived. The use of the Cauchy Formula yields fifty-six equations with seven variables, including thickness, and thus an iterative approach is required to determine thickness. The Marquardt Minimization Algorithm is used during these iterations to determine the thickness that gives the lowest chi-square (Χ²) value, and is hence the most reliable thickness result.

The technique of ellipsometry was invented by Paul Drude in 1887 who used it to determine the dielectric function of various metals and dielectrics. For 75 years following Drude's pioniering work only a handful of ellipsometric studies were done. In the late 1960's ellipsometry experienced a renaissance thanks to the availability of computers for numeric processing. It has since become one of the most important and powerful tools for the characterization of optical properties, in particular, of thin-film- and multi-layered materials. In the visible, NIR, and UV, this technique is particularly well suited to semiconductors and semiconductor based structures. Ellipsometers are widely applied in industry for characterization and on-line quality control.

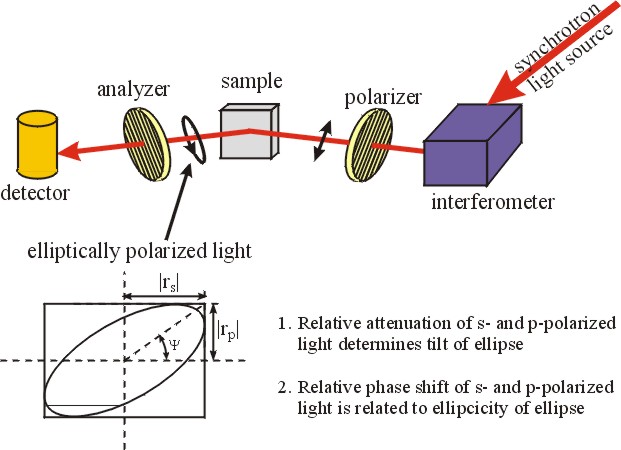
More recently, the spectral range of the ellipsometric studies has been extended to the far-infrared regime. First attempts in this direction have been undertaken by Rösseler in the 1970's. The main experimental problem in the far-infrared spectral range is the absence of intense and brilliant light sources. We have circumvented this problem by making use of a synchrotron light source, which provides by about three orders of magnitude more brilliant light in the far-infrared as compared to conventionally available light sources, like mercury arc lamps [2].

---

References:

1. C. Bernhard, T. Holden, A. Golnik, C.T. Lin and M. Cardona, "Far-infrared c-axis conductivity of flux-grown Y_1-xPr_xBa₂Cu₃O₇ single crystals studied by spectral ellipsometry", accepted for publication in Phys. Rev. B.  
2. http://academic.brooklyn.cuny.edu/physics/holden/ellips.jpg