Manual for previous SnPM versions

../SnPM_Central

A Worked fMRI Example

This page...

introduction

example data

background

Without variance smoothing

With variance smoothing

SnPM pages...

manual

PET example

fMRI example

FSL users

New SnPM example

In this section, we analyze multi-subject event-related fMRI data with the SnPM software. The aim of this example is:

Give another example to demonstrate the steps of an SnPM analysis by analyzing the fMRI data.

The same set of data have also been analyzed by SPM. The details can be found at SPM website ("fMRI: multi-subject (random effects) analyses - Canonical" data set).

The reference is: Henson, R.N.A, Shallice, T., Gorno-Tempini, M.-L. & Dolan, R.J (2002). Face repetition effects in implicit and explicit memory tests as measured by fMRI. Cerebral Cortex, 12, 178-186.

We will give two standard methods to analyze the data by using nonparametric methods:

Without smoothed variance t
With Smoothed variance t

The Example Data

The data are from a study on face repetition effects in implicit and explicit memory tests (Henson et al. 2002; see above).

In this study, twelve volunteers (six male; aged 22-42 years, median 29 years) participated in the experiment. Faces of famous and nonfamous people were presented to the subjects for 500 ms, and replaced by a baseline of an oval chequerboard throughout the interstimulus interval. Each subject was scanned during the experiment and his or her fMRI images were obtained.

Each subject's data were analyzed, creating a difference image between faces and chequerboad (baseline) watchings. So each image here is the contrast image for each subject.

Under the null hypothesis we can permute the labels of the effects of interest. One way of implimenting this with contrast images is to randomly change the sign of each subject's contrast. This sign-flipping approach can be justified by a symmetric distribution for each voxel's data under the null hypothesis. While symmetry may sound like a strong assumption, it is weaker than Normality, and can be justified by a subtraction of two sample means with the same (arbitrary) distribution.

Hence the null hypothesis here is:
H₀: The symmetric distribution of (the voxel values of the) subjects' contrast images have zero mean.

Exchangeability of Second Level fMRI Data

fMRI data presents a special challenge for nonparametric methods. Because fMRI data exhibits temporal autocorrelation, an assumption of exchangeability of scans within subject is not tenable. However, to analyze a group of subjects for population inference, we need to only assume exchangeability of subjects. The conventional assumption of independent subjects implies exchangeability, and hence a single exchangeability block (EB) consisting of all subjects.

(On a technical note, the assumption of exchangeability can actually be relaxed for the one-sample case considered here. A sufficient assumption for the contrast data to have a symmetric distribution, is for each subject's contrast data to have a symmetric but possibly different distribution. Such differences between subjects violates exchangeability of all the data; however, since the null distribution of the statistic of interest is invariant with respect to sign-flipping, the test is valid.)

Nonparametric Analysis

(Without smoothed variance t)

You can implement a nonparametric random effects analysis using the SnPM software which you can download from http://www.fil.ion.ucl.ac.uk/spm/snpm/.

First follow the instructions on the above web page to download and install SnPM (don't forget the patches !).

Then, in matlab (in a new directory !) type

 
snpm

SnPM is split up into three components (1) Setup, (2) Compute and (3) Results.

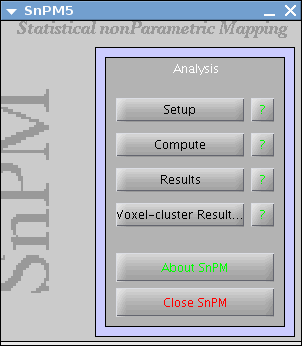
SnPM Three components Page

First click on

Setup

Then type in the following options (your responses are in square brackets). Select design type [Multisub: One sample T test on differences; 1 condition] Select all scan files from the corresponding directory in a window as below [con_0006.img -> con_0017.img] 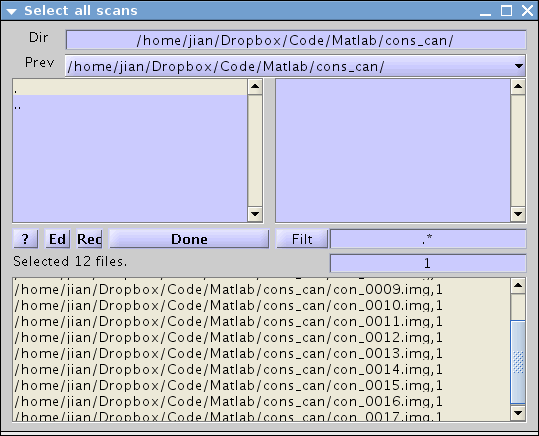Select all scans

Number of confounding covariates [0] 4096 Perms. Use approx test ? [No]

(typically, with fewer than 5000 Perms your computer should be quick enough to use an exact test - ie. to go through all permutations)

 
FWHM(mm) for Variance smooth [0]

See below (and http://www.fil.ion.ucl.ac.uk/spm/snpm/) for more info on the above option.

 
Collect Supra-Threshold stats [Yes]
 
Define the thresh now? [No]

Collecting suprathreshold statistics is optional because the file created is huge; it is essentially the "mountain tops" of the statistic image of every permutation is saved. Say "No" if you want to save disk space and time.

 
Select Global Normalisation [No Global Normalization]
      
Grand Mean Scaling  [No Grand Mean Scaling]

The above option doesn't matter because no normalisation will be done (this is specified in the next step)

 
Threshold masking [None]

Note, there's no need to use threshold masking since the data are already implicitly masked with NaN's.

Finally, the Setup Menu is as below:

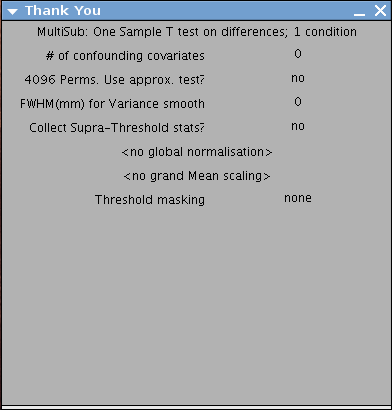
Setup Menu

SnPM will now create the file SnPMcfg.mat. and show the Design Matrix in the Graphics window.

Now click on

 
Compute

Select the file (SnPMcfg.mat) as below 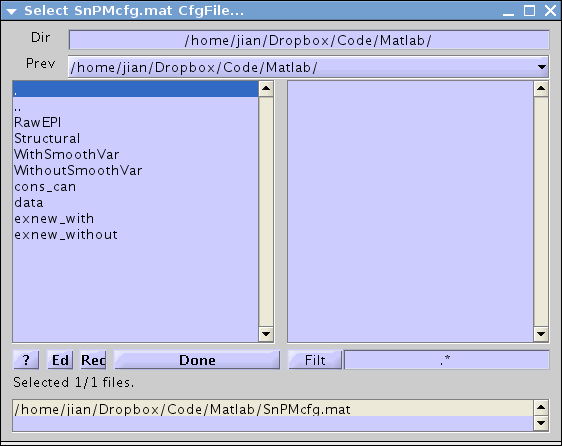Choose the file to compute

The computation should take between 5 and 10 minutes depending on your computer.In one of the SnPM window, it will show the percentage of the completeness, and in the matlab window, the permutation step that is being performed will be listed.

Note that it shows how many minutes and seconds spent on each permutation. The number in parentheses is the percentage of time spent on variance smoothing. Since we choose no variance smoothing, this is 0%.

Finally click on

 
Results

Select the SnPM.mat file in the corresponding directory as below, select SnPM.mat

In the menu, choose the following options:

 
 
 
Positive or negative effects?: (+ve)
 
Write filtered statistic img?: (yes)
 
Filename?: SnPMt_filtered 
 
Results for which img? (T)
 
Voxelwise: Use Corrected thresh (FWE) 
 
FWE-Corrected p value threshold: (0.05)

Finally, the SnPM PostProcess menu will be as below,

SnPM will then show the distribution of the maximum t-statistic.

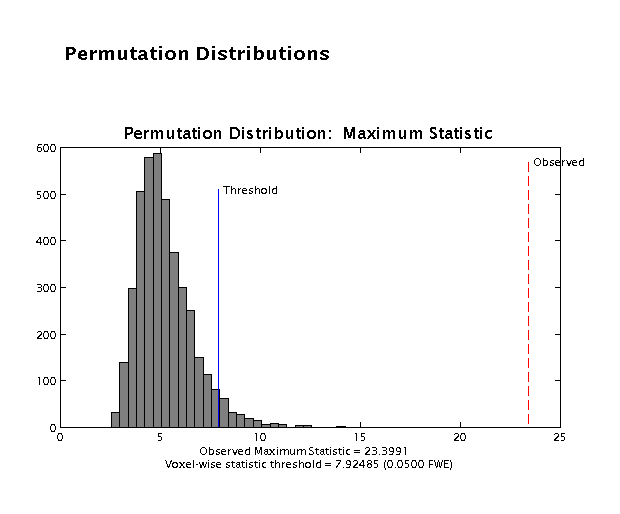
Results: permutation distributions

A small dialog box will come out and ask you to review the permutation distributions and to choose either 'Print & Continue' (to print the histogram to spm_date.ps file and then to continue) or just 'Continute' only. Click on one of the two buttons.

On next page, SnPM will then show the permutation distributions of the uncorrected P values, together with a FDR plot.

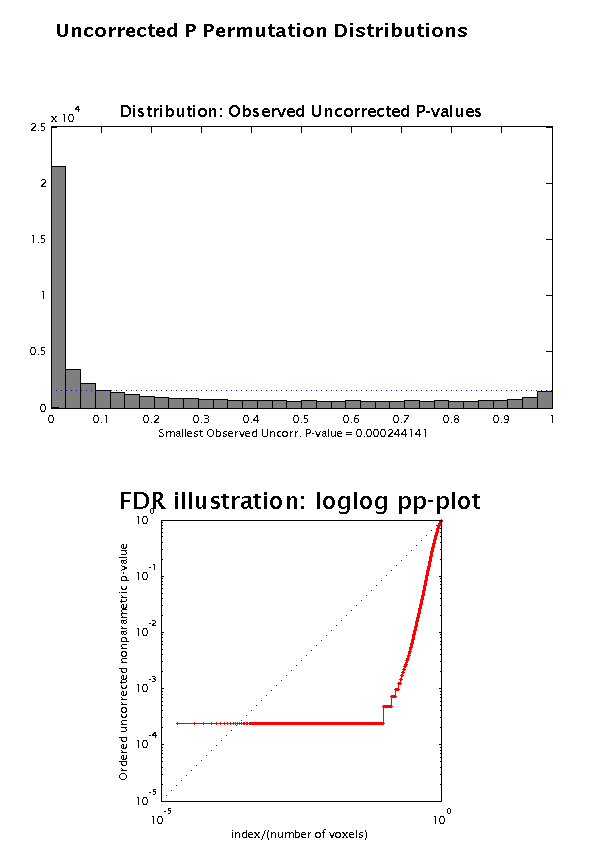
Results: Uncorrected P Permutation Distributions and FDR Plot

Choose to print the page to spm_date.ps file and then continue or to continue directly by using the prompted small dialog box.
On next page, SnPM will then plot a MIP of those voxels surviving the SnPM critical threshold (this value is displayed at the bottom of the image and for this data set should be 7.92).

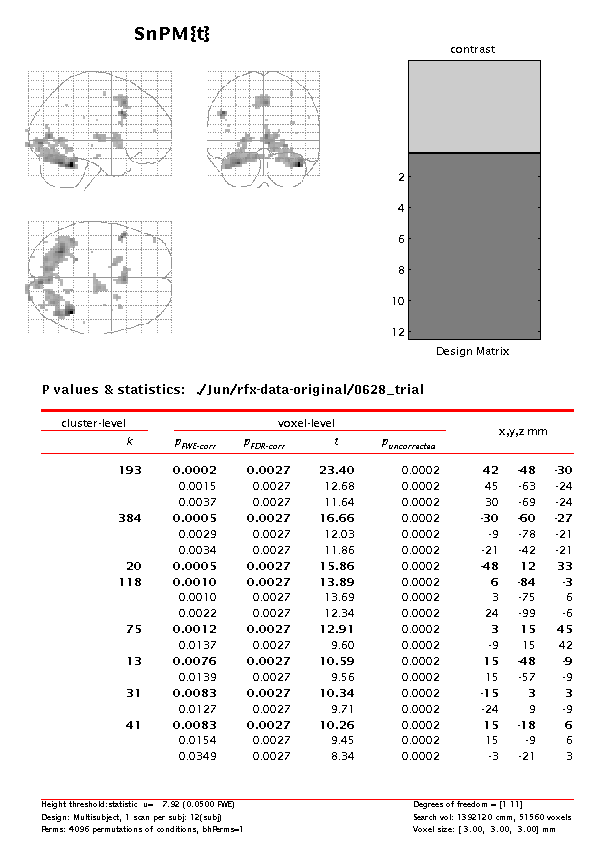
Results: MIP and et.c.

You can then use this value in SPM (in the RESULTS section, say 'No' to corrected height threshold, and then type in 7.9248 for the threshold) and take advantage of SPMs rendering routines (not available in SnPM).

Note that the SnPM threshold is lower than the SPM threshold (9.07). Consequently, SnPM shows more active voxels.

...to top

Nonparametric Analysis

(With smoothed variance t, Pseudo-t)

Note that the result just obtained looks "jaggedy". That is, while the image data is smooth (check the con* images), the t statistic image is rough. A t statistic is a estimate divided by a square root of the variance of the estimate, and this roughness is due to uncertainty of the variance estimate; this uncertainty is especially bad when the degrees of freedom are low (here, 11). By smoothing the variance before creating a t ratio we can eliminate this roughness and effectively increase our degrees of freedom, increasing our power.

Create a new directory for the smoothed variance results.

First click on

 
Setup

Then type in the following options (your responses are in square brackets).

 
[Multisub: One Sample T test on differences; 1 condition]
 
Select all scans [con_0006.img -> con_0017.img]
 
Number of confounding covariates [0]
 
4096 Perms. Use approx test ?   [No]  
 
FWHM(mm) for Variance smooth [8]

A rule of thumb for the variance smoothing is to use the same FWHM that was applied to the data (which is what we've used here), though a little as 2 x VoxelSize may be sufficient.

 
Collect Supra-Threshold stats [Yes]
 
Select Global Normalisation [No Global Normalization]
 
Define the thresh now? [No] 
 
Grand Mean Scaling [No Grand Mean Scaling]

Again, this doesn't matter because no normalisation will be done.

 
Threshold masking [None]

The final Setup Menu will be as below,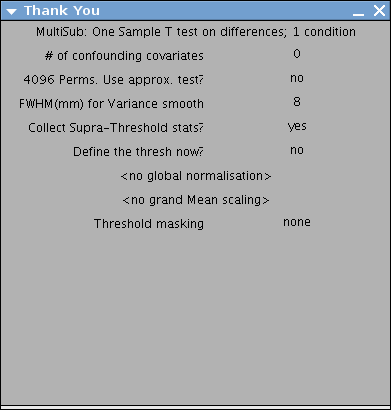

SnPM will now create the file SnPMcfg.mat. In the Graphics window, the design matrix will be shown.

Now click on

 
Compute

Select the file (SnPMcfg.mat)

In the matlab window, the permutation step that is being performed will be listed.

Computing Process

Note that it shows how many minutes and seconds spent on each permutation. The number in parentheses is the percentage of time spent on variance smoothing. Compare this result with what we get from "Without smoothed variance t" method (0% in that case).

The above computation should take between 10 and 25 minutes depending on your computer.

Finally click on

 
Results

Select the SnPM.mat file

Make the following choices:

 
 
Positive or negative effects?: (+ve)
 
Write filtered statistic img?: (yes)
 
Filename?: SnPMt_filtered
 
Results for which img? (T) 
 
Write FWE-corrected p-value img?: (yes)
 
Use corrected threshold?: (FWE)
 
Voxelwise FWE-Corrected p value threshold: (0.05)

The final Results Setup Menu will be as below,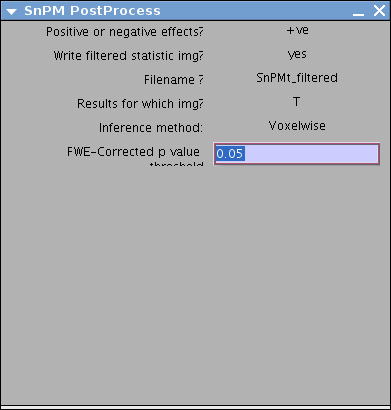

SnPM will then show the distribution of the maximum *pseudo* t-statistic, or smoothed variance t statistic as below.

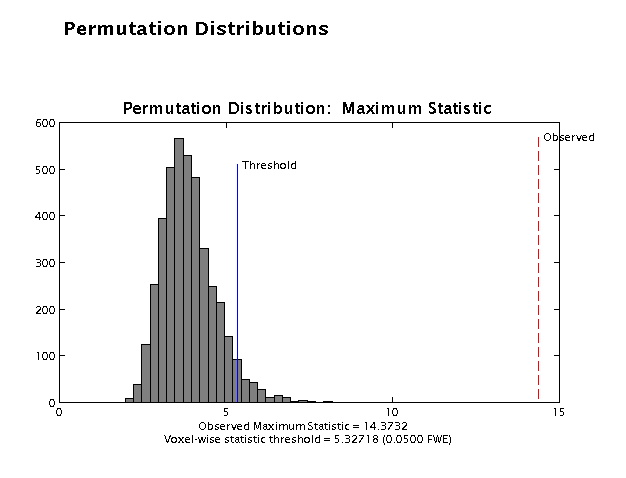
Setup Menu

On next page, SnPM will then show the permutation distributions of the uncorrected P values, together with a FDR plot.

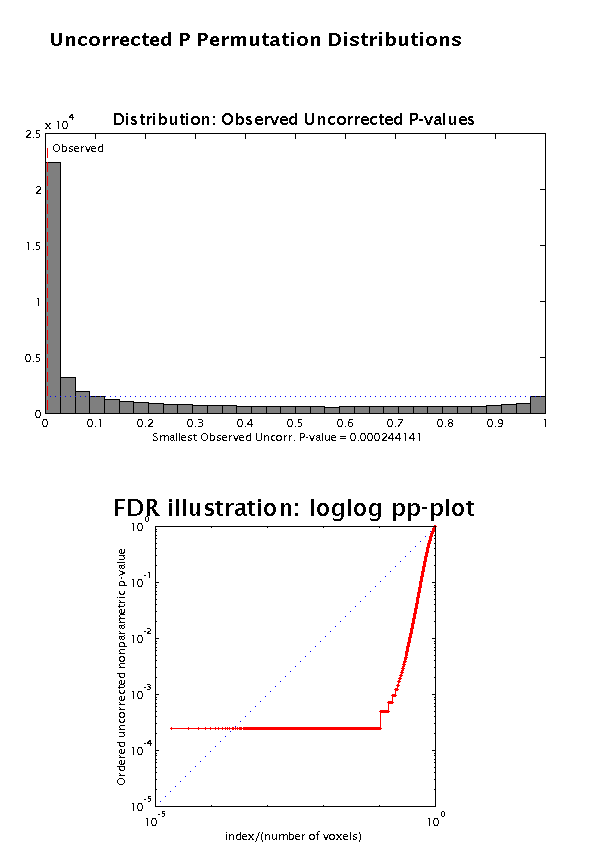
Results: Uncorrected P Permutation Distributions and FDR Plot

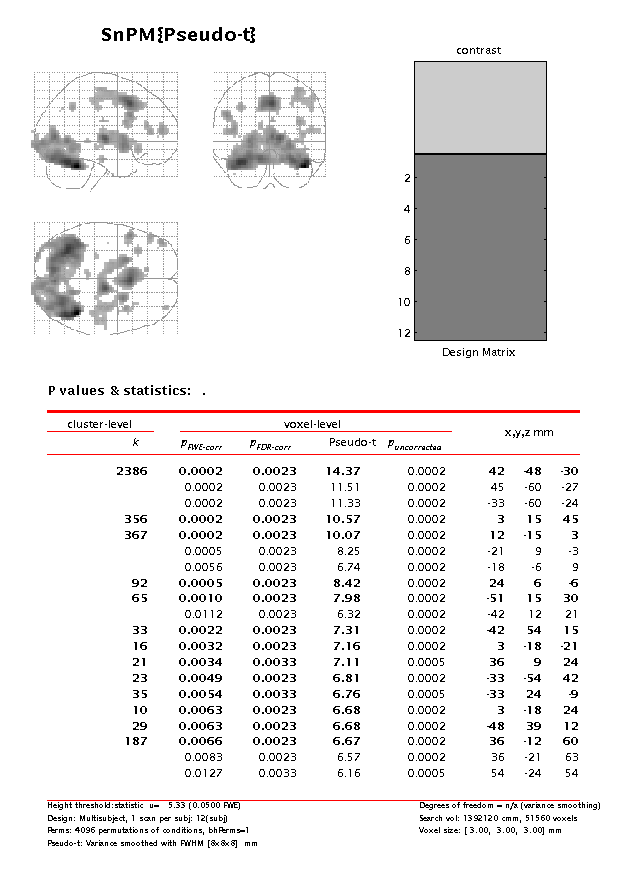
Setup Menu

Observe how there are both more suprathreshold voxels, and that the image is smoother. For example, note that the anterior cingulate activation (3,15,45) is now 356 voxels, as compared with 75 with SnPM{t} or 28 with SPM{t}.

Very important!!! This is not a t image. So you cannot apply this threshold to a t image in SPM. You can, however, create overlay images with the following:

Use 'Display' to select the image you would like for a background. Via the keyboard only you could do...
```
 
Img =  spm_get(1,'.img','select background reference');
spm_image('init',Img)
```

Create filtered image with NaN's instead of zero's.

 
In    = 'SnPMt_filtered';
Out   = 'SnPMt_filteredNaN';
f     = 'i1.*(i1./i1)';
flags = {0,0,spm_type('float')};
spm_imcalc_ui(In,Out,f,flags);

Ignore the division by zero errors.

Overlay the filtered image

spm_orthviews('addimage',1,'SnPMt_filteredNaN')

...to top

Back to main SnPM page
SnPM by Andrew Holmes of the Astra Zeneca
& Tom Nichols of University of Michigan Biostatistics department
SnPMauthors at <snpm-authors at umich.edu>

Neuroimaging
Statistics

Contact Info

Room D0.03
Deptment of Statistics
University of Warwick
Coventry
CV4 7AL
United Kingdom

Tel: +44(0)24 761 51086
Email: t.e.nichols 'at' warwick.ac.uk
Web: http://nisox.org
Blog: NISOx blog

@ten_photos on Twitter

Handbook of fMRI Data Analysis by Russ Poldrack, Thomas Nichols and Jeanette Mumford