Coulomb Blockade

We've dealt with the conductance of a quantum wire on the page above, now let's consider the conductance of a quantum dot. For simplicity, we assume a transistor-like geometry.

Conduction through this system occurs via sequential tunnelling of an electron from the source to the quantum dot, and then from the quantum dot to the drain. However, the addition of the electron to the quantum dot will substantially change the energy of the dot, in particular, the Coulomb repulsion of the added electron blocks the addition of further electrons.

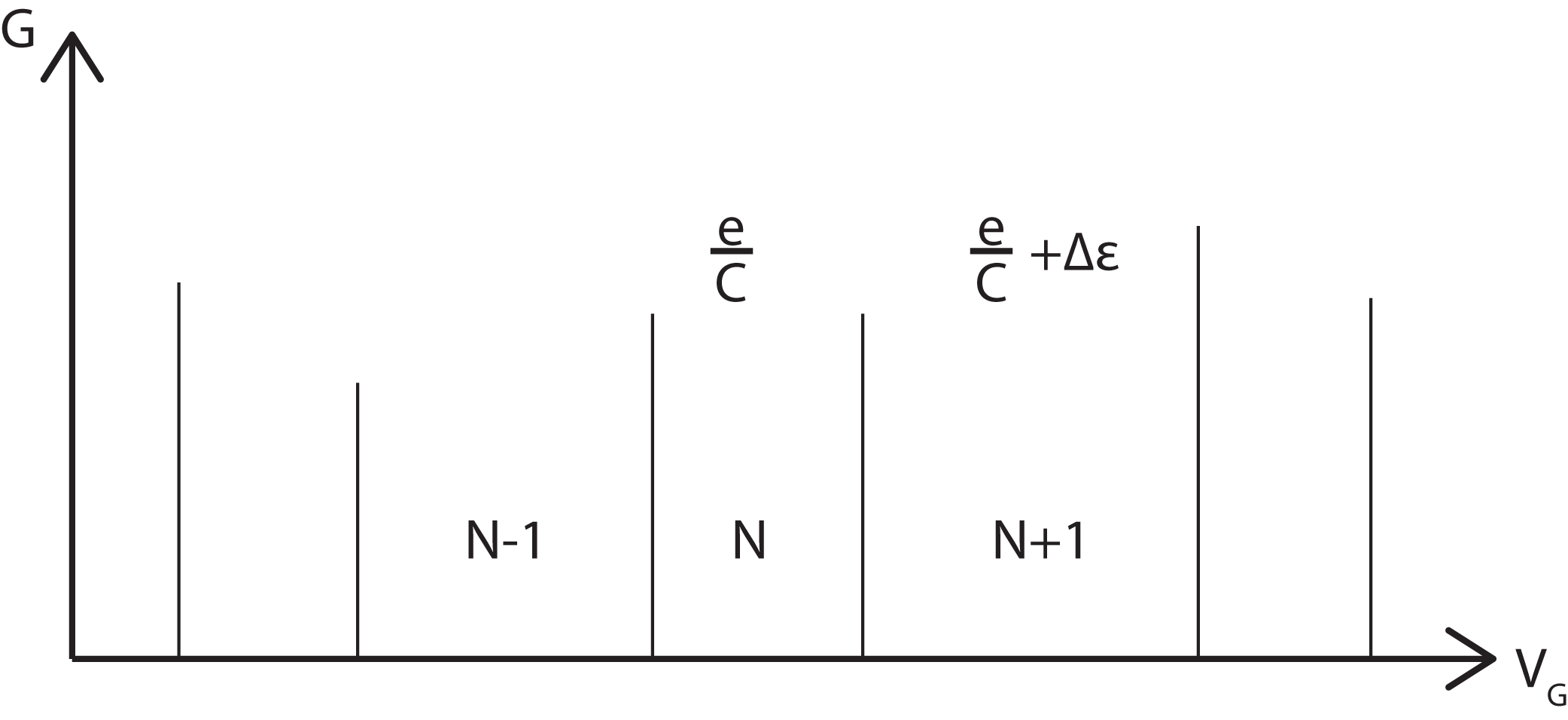
Measurements of such quantum dots show that most of the time this system does not conduct, but there do exist conductance peaks which are fairly regularly spaced. This is called Coulomb Blockade, where the device is acting a a single electron transistor.

This behaviour is explained below:

The energy of N electrons on the quantum dot can be split into contributions from the energy levels and the charging energy

$E_N=\epsilon_1+\epsilon_2+...+\epsilon_N + \frac{(Ne)^2}{2C}$

with an extra electrostatic contribution from the gate electrode,

$\alpha V_GN$

where α is the capacitance coupling of the dot to the gate.

The number of electrons on the quantum dot is determined by the chemical potential, if

$E_N+\alpha V_GN<\mu<E_{N+1}+\alpha V_G(N+1)$

then there will be N electrons on the quantum dot.

So the gate voltage gives us control over the number of electrons on the quantum dot.

The energy of N+1 electrons is

$E_{N+1}=\epsilon_1+\epsilon_2+...+\epsilon_{N+1}+\frac{(N+1)^2e^2}{2C}$

The difference is energy between N and N+1 is therefore

$\Delta E_{N\rightarrow N+1}E_{N+1}-E_{N}=\epsilon_{N+1}+(2N+1)\frac{e^2}{2C}$

When the energy of N electrons is equal to the energy of N+1 electrons then the dot can have an occupancy of either. At this point conduction can occur via sequential tunnelling of single electrons from the source to the dot to the drain, with the occupancy of the dot switching from N to N+1. In between these degeneracy points conductance is blocked by the charging energy and level spacing. Hence the separation between conductance peaks in this model given by

$\alpha\Delta V_G=\Delta E_{N\rightarrow N+1}-\Delta E_{N-1\rightarrow N}$

$=\epsilon_{N+1}-\epsilon_N+\frac{e^2}{C}$

$=\Delta\epsilon +\frac{e^2}{C}$

We can thus sketch the conductance as: