Let us consider a metal wire connected to two contact electrodes. The wire will have finite length and width. What do we expect to happen as the length of the wire is decreased?

Classically we would expect the resistance of the wire to decrease linearly with length, according to the formula

However, once L is decreased below the mean free path of an electron there can be no scattering, which in turn means that the resistance, R, can not decrease further. Thus we see the resistance of the wire plateaux, as shown by the dashed line in the figure below. This base resistance comes from the contacts.

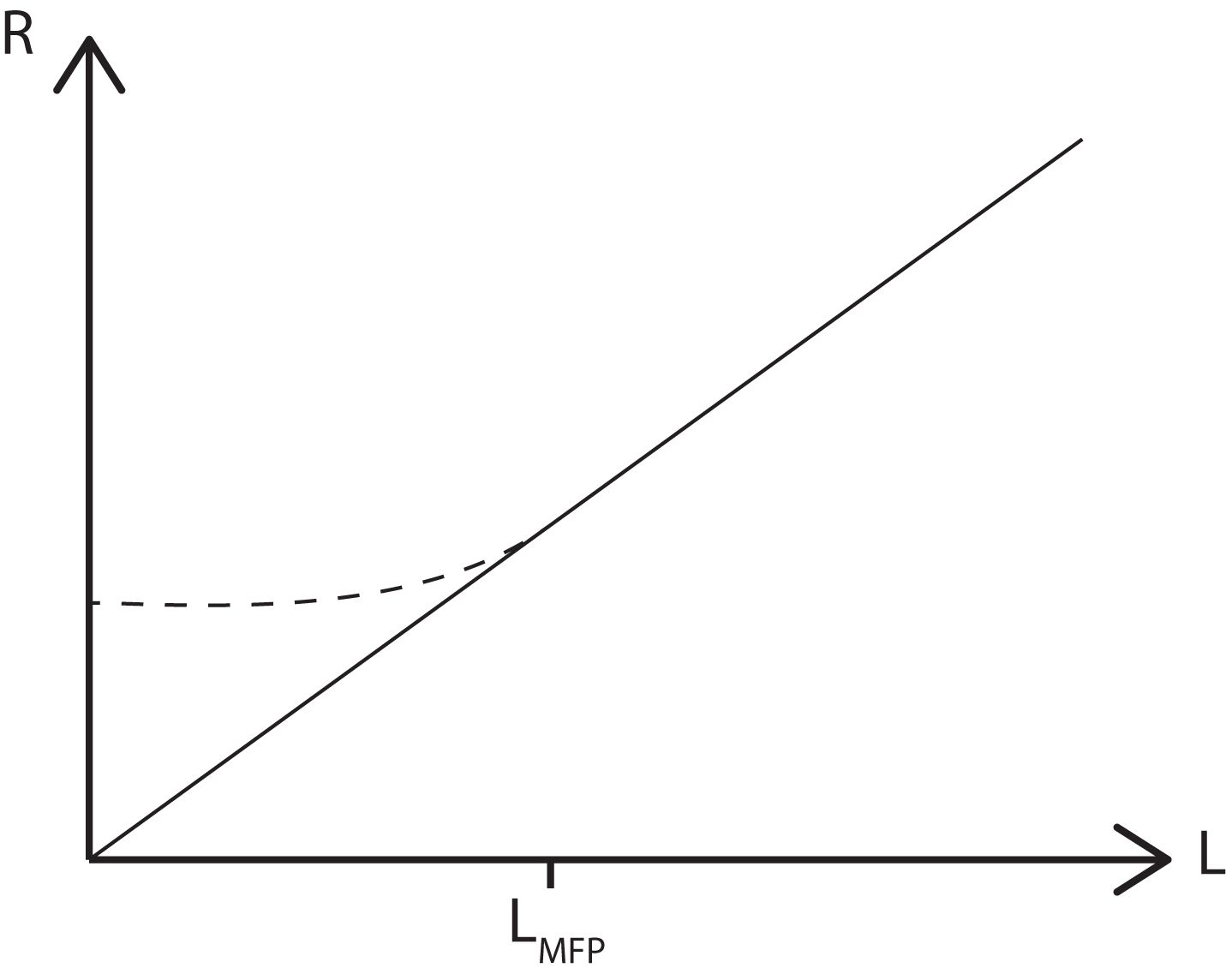
This region in which the length scale ≤ mean free path is known as the Ballistic Conductance regime. Let us now consider the conductance of the wire as its area is decreased.

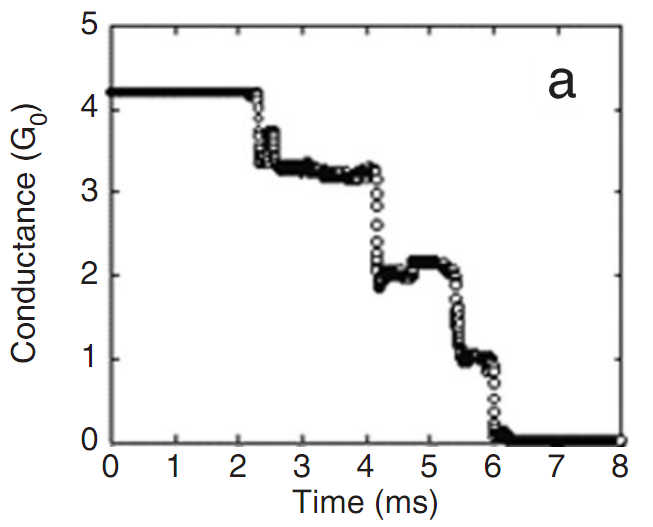
Once again according to classical physics we expect to see the conductance decrease as a linear function of A. However, what we actually see is a series of steps in the conductance, each with a height 2e²/h.

One can begin to understand the origins of this 2e²/h  term by viewing the dimensional constriction as a 1D wire connecting two electron reservoirs, with a chemical potential of μ₁ and μ₂ respectively.

The 1D current, I, is obviously equal to the current density, j, which is given by 

where v is the electron velocity and dn/dε is the density of states. In 1D, dn/dε = 2/hv, with the factor of two stemming from the fact that the spin-up and spin-down modes are degenerate.

(μ₁- μ₁) = -eV, where V is the voltage between the two reservoirs, the resulting conductance is given by

The complete description of this behaviour is given by the Landauer-Buttiker formula

were T is the transmittance. The derivation of this formula is quite complex and can be found in reference [2].

Reference

• S. Datta, Electrical Transport in Mesoscopic Systems, Cambridge University Press, 1997.
• R. Saito, Physical Properties of Carbon Nanotubes, Imperial College Press, 1998.
• H.D. Cornean et al, Advances Materials (2004).