Superconductivity

A Brief History of Superconductivity

The phenomenon of superconductivity was first observed by Kamerlingh Onnes in Leiden in 1911[1] . In the superconducting state the dc electrical resistivity is zero.
	Heike Kamerlingh Onnes, was awarded the 1913 Nobel Prize in Physics for his discovery of superconductivity.

.	The magnetic properties exhibited by superconductors are just as dramatic. If a type I superconductor is placed in a magnetic field below a critical value H_c, then cooled through its superconducting transition temperature, (T_c), the magnetic flux originally present in the sample is ejected from the specimen. This is called the Meissner effect [2].
A magnet floating above a disc of ceramic superconductor due to a combination of flux pinning and flux expulsion.

If a type II superconductor is cooled below T_c in a magnetic field less than its lower critical field, (H<H_c1), it will also enter the Meissner state. For fields above the lower critical field H_c1 but below an upper critical field H_c2, (H_c1<H<H_c2), type II superconductors enter a mixed state in which the material is threaded by an array of lines of magnetic flux forming an Abrikosov or flux line lattice [3].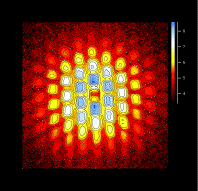

The hexagonal arrangement of magnetic flux lines in pure Nb imaged using neutrons

	The superconducting state results from an ordering of the conduction electrons into Cooper pairs via an electron-phonon exchange coupling. The nature and origin of this ordering was explained by Bardeen, Cooper, and Schrieffer (BCS). All elemental and most alloy superconductors are s-wave BCS superconductors [4].
John Bardeen, Leon Cooper, and J. Robert Schrieffer, 1972 Nobel laureates for their BCS theory of superconductivity.

Under suitable conditions remarkable macroscopic quantum mechanical effects associated with the tunnelling of the superconducting electron pairs are observed. These include the ac and dc Josephson effects [5]. SQUIDs (superconducting quantum interference device) are now used in applications.
	A Quantum Design thin film SQUID sensor.

K. Alex Muller and J. Georg Bednorz from IBM Zurich discovered ceramic high temperature superconductors. They won the 1987 Nobel Prize in Physics.

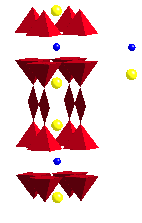
YBa₂Cu₃O_7-_d, a cuprate superconductor with a T_c of 92 K. Note the Cu-O octahedra and chains are shown in red.

The discovery by Bednorz and Müller of high temperature superconductivity in the cuprates [6] along with the observation of superconductivity in heavy fermions [7], the doped carbon fullerenes and some organic materials led to a resurgence of interest in superconductivity [8-9].


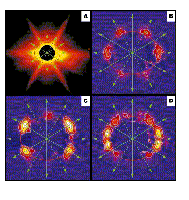
SANS data showing the change in the morphology of the flux line lattice in the heavy fermion superconductor UPt₃ [7].	There are many fullerence superconductors including Cs₃C₆₀ that has a T_c of 40 K.

Experimental evidence for exotic p and d wave superconductivity was been presented [10]. A number of materials that show a coexistence of magnetism and superconductivity have also been discovered [11]. These materials allowed us to investigate the interplay between two phenomena that are usually mutually exclusive. A whole range of subtle and fascinating new behaviours have been observed in the mixed state of superconductors including flux creep, thermally activated flux flow, flux pancakes, fll melting, reversible and irreversible behaviour, the peak effect and the generalised Fulde-Ferrel-Larkin-Ovchinnokov state to name but a few!

Superconductivity at Warwick

Since the Group was established in 1985, we have made a number of important contributions to the understanding of the physics of superconducting materials. Other Groups here at Warwick including Theory and the NMR have also worked on superconducting materials.

We began working on high temperature superconductors shortly after their discovery in 1986. We studied the unusual vibrational and structural behaviour of the compound La_1.85 Ba_0.15CuO₄ [12] and investigated the nature of the magnetic ordering in the rare earth-Ba₂Cu₃O₇ series of compounds [13].

In 1990 we began using neutron scattering to study the mixed state of the high temperature superconductors. The neutrons are diffracted by the ordered periodic distribution of the magnetic flux within the sample with contrast being provided by the variation in the magnetic induction. These diffraction experiments must be performed on a small angle diffraction instrument, since the typical lattice spacing in the available range of magnetic field with the optimum neutron wavelength leads to scattering angles of < 0.5 degree. We examined the vortex lattice structure in YBa₂Cu₃O₇ [14] and were the first to directly observe the melting and decomposition of the magnetic-flux lattice in the high-T_c superconductor Bi_2.15Sr_1.95CaCu₂O_8+x [15].

	We also began our successful crystal growth programme using an infra red image furnace as well as more conventional flux and vapour transport growth methods to produce high quality samples of many types of superconductors [16].
A single crystal of Bi₂Sr₂CaCu₂O₈ grown in the IR image furnace at Warwick.

In 1994 we began work on a new class of superconductors with the general chemical formula RNi₂B₂C (R = rare earth). The layered structure of these materials means that for some of this series there is a co-existence of long-range magnetic order with superconductivity at the same temperature. This is very rare and provided us with an exciting opportunity to study the interplay between these two phenomena.

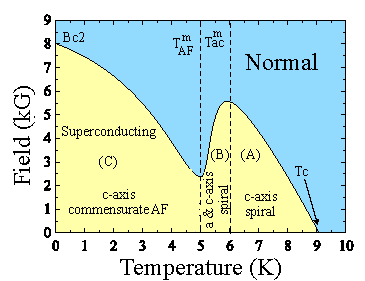
Superconducting and magnetic H-T phase diagram of HoNi₂B₂C (see Ref. 18 for more details).

The borocarbides have been shown to exhibit a rich variety of magnetic and superconducting properties [17]. We used neutron scattering, magnetometry and local Hall probes to probe the complex behaviour of the normal and superconducting states of these materials [18].

Our studies of the flux-line lattice (fll) in various superconductors have been a marked success and created considerable international interest. We refined our neutron scattering techniques and greatly enhanced the resolution with which it is possible to make such measurements. This allowed us to perform a series of very high resolution experiments examining the role of "non-local" effects in determining the distortion of the fll and permitted a completely new slant on the problem of the coexistence of magnetism and superconductivity to be developed.

An image of the flux-line lattice in the magnetic superconductor TmNi₂B₂C.

These measurements were complemented by the "global" magnetisation and resistivity studies undertaken in our laboratories. Data were also collected through a collaboration with a group in Cambridge, using a miniature Hall detector array to study the "local" magnetisation across single crystal samples. Our studies on HoNi₂B₂C demonstrated the power of this technique for understanding the role of the magnetic modulations on pinning the flux distributions.

We have shown that in CaAlSi [19], the reorientation of the FLL is due to non-local rather than multi-band effects, and examined the two-gap behaviour in Lu₂Fe₃Si₅ [20].

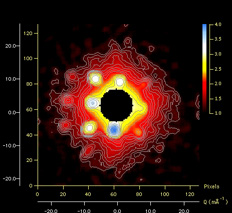
SANS diffraction patterns of CaAlSi taken at 2 K in applied magnetic fields of 97, 185, 250, and 294 Oe, respectively. (e) Schematic diagram of the FLL patterns in real-space (upper panel) and the corresponding diffraction patterns (lower panel).

We have worked on a number of superconductors with a noncentrosymmetric (NCS) structure. In noncentrosymmetric structure, i.e. a system without inversion symmetry, parity is no longer a meaningful label. The lack of inversion symmetry induces an antisymmetric spin-orbit coupling (SOC) which can lift the degeneracy of the conduction band electrons and may cause the superconducting pair wavefunction to contain a mixture of singlet and triplet spin states. The breakdown of the usual classification of superconductors into even-parity, (pseudo) spin-singlet and odd-parity, spin-triplet states means that a variety of physical effects that may previously have been forbidden are now allowed. Examples include exotic superconducting gap structures (lines or nodes in the superconducting gap), magnetoelectric effects such as a helical phase and upper critical fields exceeding the Pauli limiting field, time reversal symmetry breaking, and even topological effects and unusual surface states.

We have used muon spectroscopy to discover time-reversal symmetry breaking in the noncentrosymmetric superconductor Re₆Zr [21], in the locally NCS pnictide SrPtAs [22] and in La₇Ir₃ [23] We also examined the nature of the superconducting gap in the NCS intermetallic Nb_0.18Re_0.82[24].

We discovered that Re₃W can be reversibly switched between a centrosymmetric and noncentrosymmetric structure [25, 26], and examined the crossover from type I to type II behaviour in La(Pd/Pt)Si₃ [27].

We also made significant progress in the synthesis of single crystal NCS superconductors. This includes growth of intermetallic samples with our tetra-arc furnace and high melting point borides via the floating zone technique (please see Refs. [28 and 29].

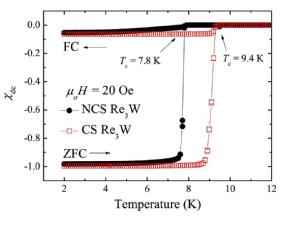Magnetic susceptibility versus temperature for the noncentrosymmetric and the centrosymmetric Re₃W measured in zero-field-cooled and field-cooled mode in an applied magnetic field of 20 Oe.

We also reported on the superconductivity in the In doped topological crystalline insulator SnTe [30], one of a new class of superconductors related to Topological Insulators, materials that have topologically protected surface states.

Recent Research at Warwick

Our most recent research [31-35] has focussed on the role of structure and spin-orbit coupling in superconductors. In conventional superconductors, we saw above that the superconductivity arises from an electron-phonon coupling of electrons to form Cooper pairs, with a single, s-wave, isotropic gap. In unconventional materials, the Cooper pairs may be coupled by other interactions, the pair wave function may be an odd-parity spin-triplet, or there may be multiple superconducting bands.

Unconventional superconductivity can be found in number of different classes of materials. These include superconductors with noncentrosymmetric crystal structures, in materials with strong spin-orbit coupling, e.g., those containing 4d and 5d metals, and in systems with unusual crystallographic geometries, e.g., kagome lattice superconductors. Unconventional superconductors can exhibit a variety of physical effects including exotic superconducting gap structures (lines or nodes in the superconducting gap), upper critical fields exceeding the Pauli limit, time reversal symmetry breaking, and topological effects.

References

[1] H. Kamerlingh Onnes, Leiden Comm. 120b 122b, 124c, (1911).

[2] W. Meissner and R. Ochsenfeld, Naturwissenschaften 21, 787 (1933).

[3] A. A. Abrikosov Sov. Phys JETP 5, 1174 (1957).

[4] J. Bardeen, L. N. Cooper and J. R. Schrieffer, Phys. Rev. 106, 162 (1957); 108, 1175 (1957).

[5] B. D. Josephson Phys. Lett. 1, 251 (1962).

[6] G. Bednorz and K. A. Müller, Z. Phys. B 64, 189 (1986).

[7] G. R. Stewart Rev. Mod. Phys. 56, 755 (1984) and references therein. For more details of the data shown in the figure see, Realignment of the flux-line lattice by a change of symmetry of superconductivity in UPt₃, A. Huxley, P. Rodiere, D. M^cK. Paul, N. van Dijk, R. Cubitt and J. Flouquet, Nature 406, 160 (2000).

[8] Good introductory textbooks on superconductivity for undergraduates: M. Cyrot and D. Pavuna, Introduction to superconductivity and high-Tc materials (World Scientific, River Edge, N.J, 1992); J.R. Waldram, Superconductivity of metals and cuprates (Institute of Physics Publishing, Bristol, 1996); G. Burns, High-temperature superconductivity : an introduction (Academic Press, London,1992); C. P. Poole, H. A. Farach and R. J. Creswick, Superconductivity (Academic Press, San Diego, London, 1995).

Graduate level textbooks: D. R. Tilley and J. Tilley, Superfluidity and Superconductivity, (IOP Publishing, Bristol, 1996), 3rd ed.; Michael Tinkham, Introduction to superconductivity, (London McGraw-Hill, New York, 1975).

[9] There are many websites with useful information on superconductors including www.superconductors.org/ and a site at Oak Ridge National LabLink opens in a new window in the USA.

[10] Reconstruction from Small-Angle Neutron Scattering Measurements of the Real Space, Magnetic Field Distribution in the Mixed State of Sr₂RuO₄, P. G. Kealey, T. M. Riseman, E. M. Forgan, L. M. Galvin, A. P. Mackenzie, S. L. Lee, D. M. Paul, R. Cubitt, D. F. Agterberg, R. Heeb, Z. Q. Mao and Y. Maeno, Phys. Rev. Lett. 84, 6094 (2000).

[11] R. Nagarajan et al. Phys. Rev. Lett. 72, 274 (1994); R. J. Cava et al. Nature (London) 367, 252 (1994).

[12] Magnetic-Ordering in GdBa₂Cu₃O_6.14, H. A. Mook, D. M^cK. Paul, B. C. Sales, L. A. Boatner, L. Cussen, Physical Review B 38, 12008 (1988); Magnetic-Ordering in the High-Temperature Superconductor ErBa₂Cu₃O_7-_d, D. M. Paul, H. A. Mook, A. W. Hewat, B. C. Sales, L. A. Boatner, J. O. Ramey, and L. Cussen, Phys. Rev. B 39, 4291 (1989).

[13] Vibrational Anomalies In The Superconducting Compound La_1.85 Ba_0.15CuO₄, G. Balakrishnan, N. R. Bernhoeft, Z. A. Bowden, D. M^cK. Paul, A. D. Taylor, Nature 327, 45 (1987); Anomalous Structural Behavior Of The Superconducting Compound La_1.85Ba_0.15CuO₄, D. M. Paul, G. Balakrishnan, N. R. Bernhoeft, W. I. F. David, and W. T. A. Harrison, Phys. Rev. Lett. 58, 1976 (1987).

[14] Observation by Neutron-Diffraction of the Magnetic-Flux Lattice in Single-Crystal YBa₂Cu₃O_7-_d, E. M. Forgan, D. M^cK. Paul, H. A. Mook, P. A. Timmins, H. Keller, S. Sutton, J. S. Abell, Nature 343, 735 (1990); Small-Angle Neutron-Scattering Study of Flux Line Lattices in Twinned YBa₂Cu₃O₇, M. Yethiraj, H. A. Mook, G. D. Wignall, R. Cubitt, E. M. Forgan, D. M^cK. Paul, and T. Armstrong, Phys. Rev. Lett. 70, 857 (1993); Anisotropic Vortex Lattice in YBa₂Cu₃O₇, M. Yethiraj, H. A. Mook, G. D. Wignall, R. Cubitt, E. M. Forgan, S. L. Lee, D. M. Paul, and T. Armstrong, Phys. Rev. Lett. 71, 3019 (1993).

[15] Direct Observation of Magnetic-Flux Lattice Melting and Decomposition in the High-Tc Superconductor Bi_2.15Sr_1.95CaCu₂ O_8+x, R. Cubitt, E. M. Forgan, G. Yang, S. L. Lee, D. M. Paul, H. A. Mook, M. Yethiraj, P. H. Kes, T. W. Li, A. A. Menovsky, Z. Tarnawski, and K. Mortensen, Nature 365, 407 (1993).

[16] Single-Crystal Growth of Bi₂Sr₂CaCu₂O₈ Using an Infrared Image Furnace, G. Balakrishnan, D. M^c K. Paul, M. R. Lees, and A. T. Boothroyd, Physica C 206, 148 (1993); Superconducting Properties of Doped and Off-Stoichiometric Bi₂Sr₂CaCu₂O₈ Single-Crystals, G. Balakrishnan, D. M. Paul, and M. R. Lees, Physica B 194, 2197 (1994).

[17] Magnetic structure of TmNi₂B₂C, L. J. Chang, C. V. Tomy, D. M^cK. Paul, and C. Ritter, Phys. Rev. B 54 , 9031(1996); Anisotropic magnetic properties of TbNi₂B₂C single crystals, C. V. Tomy et al., Physical Review B 53, 307(1996); Superconductivity and Magnetism in DyNi₂B₂C Single-Crystals, C. V. Tomy, M. R. Lees, L. Afalfiz, G. Balakrishnan, and D. M. Paul, Phys. Rev. .B 52, 9186 (1995).

[18] Interaction between magnetic order and the vortex lattice in HoNi₂B₂C, C. D. Dewhurst, R. A. Doyle, E. Zeldov, and D. M^cK. Paul, Phys. Rev. Lett. 82, 827 (1999).

[19] First-Order Reorientation Transition of the Flux-Line Lattice in CaAlSi, P. K. Biswas, M. R. Lees, G. Balakrishnan, D. Q. Liao, D. S. Keeble, J. L. Gavilano, N. Egetenmeyer, C. D. Dewhurst, and D. M. Paul, Phys. Rev. Lett. 108, 077001 (2012).

[20] Two-gap superconductivity in Lu₂Fe₃Si₅: A transverse-field muon spin rotation study, P. K. Biswas, G. Balakrishnan, D. M. Paul, C.V. Tomy, M. R. Lees, and A. D. Hillier, Phys. Rev. B 83, 054517 (2011).

[21] Detection of Time-Reversal Symmetry Breaking in the Noncentrosymmetric Superconductor Re₆Zr Using Muon-Spin Spectroscopy, R. P. Singh, A. D. Hillier, B. Mazidian, J. Quintanilla, J. F. Annett, D. M. Paul, G. Balakrishnan, M. R. Lees, Phys. Rev. Lett. 112, 107002 (2014).

[22] Evidence for superconductivity with broken time-reversal symmetry in locally noncentrosymmetric SrPtAs, P. K. Biswas, H. Luetkens, T. Neupert, T. Sturzer, C. Baines, G. Pascua, A. P. Schnyder, M. H. Fischer, J. Goryo, M. R. Lees, H. Maeter, F. Bruckner, H.-H. Klauss, M. Nicklas, P. J. Baker, A. D. Hillier, M. Sigrist, A. Amato, and D. Johrendt, Phys. Rev. B 87, 180503(R) (2013).

[23] J. A. T. Barker et al. Unconventional superconductivity in La₇Ir₃ revealed by muon spin relaxation: introducing a new family of noncentrosymmetric superconductor that breaks time-reversal symmetry Phys. Rev. Lett. 115, 267001 (2015).

[25] Structure and superconductivity in two different phases of Re₃W, P. K. Biswas, M. R. Lees, A. D. Hillier, R. I. Smith, W. G. Marshall, and D. M. Paul, Phys. Rev. B 84, 184529 (2011).

[26] Comparative study of the centrosymmetric and noncentrosymmetric superconducting phases of Re₃W using muon spin spectroscopy and heat capacity measurements, P. K. Biswas, A. D. Hillier, M. R. Lees, and D. M. Paul, Phys. Rev. B 85, 134505 (2012).

[27] Investigations of the superconducting states of noncentrosymmetric LaPdSi₃ and LaPtSi₃, M. Smidman, A. D. Hillier, D. T. Adroja, M. R. Lees, V. K. Anand, R. P. Singh, R. I. Smith, D. M. Paul, and G. Balakrishnan, Phys. Rev. B 89, 094509 (2014).

[28] Crystal growth of the non-centrosymmetric superconductor Nb_0.18Re_0.82, R. P. Singh, M. Smidman, M. R. Lees, D. M. Paul, G. Balakrishnan, J. Cryst. Growth 361, 129 (2012).

[29] Crystal growth and properties of the non-centrosymmetric superconductor, Ru₇B₃, R. P. Singh, N. A. Parzyk, M. R. Lees, D. M. Paul, G. Balakrishnan, J. Cryst. Growth 395, 22 (2014).

[30] Superconducting properties of the In-substituted topological crystalline insulator SnTe, G. Balakrishnan, L. Bawden, S. Cavendish, M. R. Lees, Phys. Rev. B 87, 140507 (2013).

[31] D. A. Mayoh et al. Multigap superconductivity in chiral noncentrosymmetric TaRh₂B₂, Phys. Rev. B 98, 014502 (2018).

[32] P. K. Biswas et al. Chiral singlet superconductivity in the weakly correlated metal LaPt₃P, Nature Commun. 12, 2504 (2021).

[33] D. Das et al. Probing the superconducting gap structure in the noncentrosymmetric topological superconductor ZrRuAs, Phys. Rev. B 103, 144516 (2021).

[34] D. A. Mayoh et al. Evidence for the coexistence of time-reversal symmetry breaking and Bardeen-Cooper-Schrieffer-like superconductivity in La₇Pd₃, Phys. Rev. B 103, 024507 (2021).

[35] D. G. C. Jonas et al. Quantum muon diffusion and the preservation of time-reversal symmetry in the superconducting state of type-I rhenium, Phys. Rev. B 105, L020503 (2022).

Nobel Prize in Physics: 1913

"for his investigations on the properties of matter at low temperatures which led, inter alia, to the production of liquid helium"

Heike Kamerlingh Onnes

Nobel Prize in Physics: 1972

"for their jointly developed theory of superconductivity, usually called the BCS-theory"

John Bardeen, Leon Neil Cooper and John Robert Schrieffer

Royal Institute Video

Levitating Superconductor on a Möbius strip

Nobel Prize in Physics: 1973

"for their experimental discoveries regarding tunneling phenomena in semiconductors and superconductors, respectively"

Leo Esaki, Ivar Giaever and Brian David Josephson

Nobel Prize in Physics: 1987

"for their important break-through in the discovery of superconductivity in ceramic materials"

J. Georg Bednorz and K. Alexander Müller

Nobel Prize in Physics: 2003

"for pioneering contributions to the theory of superconductors and superfluids"

A.A. Abrikosov, V.L. Ginzburg, A.J. Leggett

100 Years of Superconductivity

Physics World: 100 Years of Superconductivity - Published in 2011- an issue of Physics World celebrating the 100^th anniversary of the discovery of superconductivity.

The Physics of Superconductors

Read more about the physics of superconductors at www.superconductors.org/