Hidden Markov Model

The Basic Framework

The standard HMM relies on 3 main assumptions:

1. Markovianity

The current state of the unobserved node $H_{t}$ depends solely upon the previous state of the unobserved variable, i.e.

$\mathbb{P}[H_{t}=h_{t}|H_{1:t-1}=\textbf{h}_{1:t-1},O_{1:t}=\textbf{o}_{1:t}] = \mathbb{P}[H_{t}=h_{t}|H_{t-1}=h_{t-1}] \hspace*{3mm}\forall\hspace*{1mm}h_{t}\in\mathbb{H}.$

2. Output Independence

The current state of the observed node $O_{t}$ depends solely upon the current state of the unobserved variable, i.e.

$\mathbb{P}[O_{t}=o_{t}|H_{1:t}=\textbf{h}_{1:t},O_{1:t-1}=\textbf{o}_{1:t-1}] = \mathbb{P}[O_{t}=o_{t}|H_{t}=h_{t}] \hspace*{3mm}\forall\hspace*{1mm}o_{t}\in\mathbb{O}.$

3. Stationarity

The transition probabilities are independent of time, i.e. $\hspace*{4mm}\forall\hspace*{1mm}t\geq0, \hspace*{1mm}s\in\{0,\dots,t\}$

$\mathbb{P}[H_{t} = j | H_{t-1} = i ] = \mathbb{P}[H_{t+s} = j | H_{t+s-1} = i ] \hspace*{3mm}\forall\hspace*{1mm}i,j\in\mathbb{H}.$

The first two assumptions are best understood when considering a graphical representation of the HMM. Directed acyclic graphs (sometimes simply referred to as DAGs) are graphs in which nodes represent random variables whilst edges represent statistical dependencies between the nodes. As can be seen below, observed nodes depend solely upon the current state of the unobserved node, which reflects Assumption 2 above. Moreover, unobserved nodes depend on the previous state of the latent variable, reflecting the Markovian nature of the latent variable (Assumption 1 above). Indeed, if the latent variable is considered in isolation, then this forms a Markov chain.

HMM

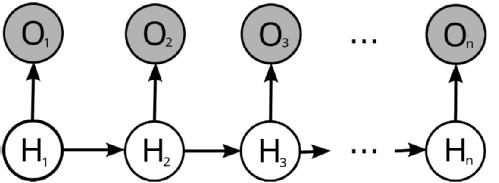
Assumptions 1 to 3 allow for an easy factorisation of the joint distribution of $H_{1:T}$ and $O_{1:T}$ . Namely, if we consider the above figure, we note that $H_{1}$ is the only node which doesn't depend on any other node in the diagram. Thus we can extract the term $\mathbb{P}[H_{1}]$ from the joint distribution and condition the remaining nodes in the graph on $H_{1}$ . As $O_{1}$ depends solely upon $H_{1}$ , we can extract the factor $\mathbb{P}[O_{1}|H_{1}]$ and condition the remaining nodes in the graph on $O_{1}$ . Proceeding iteratively in this manner, we observe that we get the following decomposition of the joint distribution

$\mathbb{P}[H_{1:T},O_{1:T}] &= \mathbb{P}[H_{1}]\mathbb{P}[H_{2:T},O_{1:T}|H_{1}] = \mathbb{P}[H_{1}]\mathbb{P}[O_{1}|H_{1}]\mathbb{P}[H_{2:T},O_{2:T}] \nonumber \\ &= ... = \mathbb{P}[H_{1}]\mathbb{P}[O_{1}|H_{1}]\prod_{i=2}^{T}\mathbb{P}[H_{i}|H_{i-1}]\mathbb{P}[O_{i}|H_{i}]$

where we have omitted the values which $H_{1:T}$ and $O_{1:T}$ assume to reduce on encumbrance. This decomposition is particularly useful as it allows us to describe the entire model solely via two matrices, which are easily interpreted and intuitive: the transition matrix

$T := (a_{ij})_{(i,j)\in\mathbb{H}^{2}}=\Big(\mathbb{P}[H_{t}=j|H_{t-1}=i]\Big)_{(i,j)\in\mathbb{H}^{2}}$

which gives the transition probability from state $i$ to state $j$ for the unobserved variable, and the emission matrix

$E:=(b_{j}(k))_{(j,k)\in\mathbb{H}\times\mathbb{O}}=\Big(\mathbb{P}[O_{t}=k|H_{t}=j]\Big)_{(j,k)\in\mathbb{H}\times\mathbb{O}}$

which gives the probability of the observed variable emitting symbol $k$ given the current hidden state is $j$ .

Inference - the Baum-Welch Algorithm

Having derived the modelling framework, we now shift our focus to conducting inference on the matrices $T$ and $E$ . To this end, we shall outline the Baum-Welch algorithm which consists of 3 main steps: the Forward pass, the Backward pass and the EM step. The Baum-Welch algorithm turns out to be a particular instance of the EM algorithm, whose major advantage is that estimates are re-calculated at each iteration, and each subsequent re-estimate is as good as, if not better than, the previous estimate. We now move on to explaining the three parts constituting the Baum-Welch algorithm, before providing a pseudocode highlighting the main steps of the algorithm.

The Forward Pass

The Forward Pass computes the likelihood of a particular sequence of observations. The challenge is naturally the fact that the observed sequence depends on the hidden sequence (which we do not observe). Thus we need to condition on the values assumed by the hidden variable and then average over all possible configurations for the hidden sequence. Using the notation we introduced above, we have that

$\mathbb{P}[O_{1:T}=\textbf{o}_{1:T}] = \sum_{\textbf{h}_{1:T}\in\mathbb{H}^{T}}\mathbb{P}[O_{1:T}=\textbf{o}_{1:T}|H_{1:T}=\textbf{h}_{1:T}]\mathbb{P}[H_{1:T}=\textbf{h}_{1:T}].$

Clearly, as the number of elements in $\mathbb{H}$ increases and as $T$ grows, the number of computations required to calculate the above quantity in a reasonable amount of time becomes very quickly impossible for most machines. To this end, we introduce the forward trellis $\alpha_{t}(i)$ from dynamic programming, which represents the probability of being in state $i$ after observing the first $t$ observations, i.e. $\alpha_{t}(i) = \mathbb{P}[O_{1:t}=\textbf{o}_{1:t},H_{t}=i]$ . The reason why the forward trellis is so useful is that it satisfies a neat recursion, namely

$\alpha_{t}(j) = \sum_{i\in\mathbb{H}}\alpha_{t-1}(i)a_{ij}b_{j}(o_{t}) \hspace*{5mm}\forall\hspace*{1mm}t\leq T .$

The Backward Pass

The backward pass concerns itself with computing the probability of observing a sequence of states for the observed variable in the future, given the current hidden state. We denote this as $\beta_{t}(i) = \mathbb{P}[O_{t+1:T}=\textbf{o}_{t+1:T}|H_{t}=i]$ , and as for the Forward Pass we have a neat recursion which simplifies computation:

$\beta_{t}(i) = \sum_{j\in\mathbb{H}}\beta_{t+1}(j)a_{ij}b_{j}(o_{t+1}).$

The Expectation-Maximisation Step

As the name implies, the EM step will have two main steps: taking expectations and subsequently maximising. We start with re-estimating the transition matrix for the hidden variable T.

Re-estimating T

Define $\hat{a}_{ij}$ to be the expected number of transitions from state i to state j for the hidden random variable, normalised by the expected number of transitions going out of state i for the hidden variable. Computing $\hat{a}_{ij}$ can be simplified by introducing an auxiliary variable $\xi_{t}(i,j) = \mathbb{P}[H_{t}=i,H_{t+1}=j|O_{1:t}=\textbf{o}_{1:t}]$ , which denotes the probability of the hidden state taking the values i and j at times t and t+1 respectively, given the observations $O_{1:t}$ up to time t assume the values $\textbf{o}_{1:t}$ . Indeed, if we have computed $\xi_{t}(i,j) \hspace*{2mm}\forall\hspace*{1mm}t\leq T$ , then we can compute $\hat{a}_{ij}$ since

$\hat{a}_{ij} = \frac{\sum_{t=1}^{T-1}\xi_{t}(i,j)}{\sum_{t=1}^{T-1}\sum_{k\in\mathbb{H}}\xi_{t}(i,k)}$

using the Markov property. So we can now consider computing the $\xi_{t}(i,j)$ , for then we have obtained the re-estimate $\hat{a}_{ij}$ . To compute this, we make use of the definition of conditional probability together with Assumptions 1 and 2 to get

$\xi_{t}(i,j) = \frac{\alpha_{t}(i)a_{ij}b_{j}(o_{t+1})\beta_{t+1}(j)}{\sum_{k\in\mathbb{H}}\alpha_{t}(k)\beta_{t}(k)}.$

Re-estimating E

We apply the same reasoning as above, namely we let $\hat{b}_{j}(k)$ be the expected number of times we observe symbol k when the hidden variable is in state j, divided by the expected number of times the hidden variable is in state j. Once again, computing this quantity can be simplified by introducing an auxiliary variable. Indeed, let $\gamma_{t}(j):=\mathbb{P}[H_{t}=j|O_{1:T}=\textbf{o}_{1:T}]$ , then we observe that

$\gamma_{t}(j) = \frac{\alpha_{t}(j)\beta_{t}(j)}{\sum_{k\in\mathbb{H}}\alpha_{t}(k)\beta_{t}(k)}$

and thus, as for the $\hat{a}_{ij}$ above, we get that

$\hat{b}_{j}(k) = \frac{\sum_{t=1\text{ s.t. }O_{t}=k}^{T}\gamma_{t}(j)}{\sum_{t=1}^{T}\gamma_{t}(j)}.<br />$

Baum-Welch Algorithm Pseudocode

Initialise

$T:=(a_{ij})_{(i,j)\in\mathbb{H}^{2}}$, $E:=(b_{j}(k))_{(j,k)\in\mathbb{H}\times\mathbb{O}}$

While $d(T^{(t)},T^{(t+1)}) > \varepsilon$ \texttt{ AND } $d(E^{(t)},E^{(t+1)}) > \varepsilon$

Compute

$\xi_{t}(i,j) = \frac{\alpha_{t}(i)a_{ij}b_{j}(o_{t+1})\beta_{t+1}(j)}{\sum_{k\in\mathbb{H}}\alpha_{t}(k)\beta_{t}(k)}$ $\forall\hspace*{1mm}t, i, j$

$\gamma_{t}(j) = \frac{\alpha_{t}(j)\beta_{t}(j)}{\sum_{k\in\mathbb{H}}\alpha_{t}(k)\beta_{t}(k)}$ $\forall\hspace*{1mm}t, j$

Compute

$\hat{a}_{ij} = \frac{\sum_{t=1}^{T-1}\xi_{t}(i,j)}{\sum_{t=1}^{T-1}\sum_{k\in\mathbb{H}}\xi_{t}(i,k)}$

$\hat{b}_{j}(k) = \frac{\sum_{t=1\text{ s.t. }O_{t}=o_{t}}^{T}\gamma_{t}(j)}{\sum_{t=1}^{T}\gamma_{t}(j)}$

Return $\tilde{T}, \tilde{E}$

We point out that in the above, $d(\cdot,\cdot)$ is some metric defined on matrices, $\varepsilon$ is some pre-specified threshold, $T^{(t)}$ and $E^{(t)}$ denote the re-updated estimates of T and E at the $t^{\text{th}}$ iteration, and $\tilde{T}$ and $\tilde{E}$ represent the final estimates for T and E.

MASDOC - Mathematics and Statistics Doctoral Training Centre