Theoretical models used

 These models follow on from the early work of Efros and Efros (1982). Two of the conditions which have been treated in detail are R >>aB and R<< aB, where aB is the bulk exciton Bohr radius. Einevoll (1992) has listed four main procedures.

   A.  The EMA usually involving parabolic bands.

 

 Efros and Efros (1982) developed an idealized model, with infinite potential wells at the crystallite surface, and excluded Coulomb terms.

      The finite size of microcrystallites leads to an increase in the kinetic energy of confined quasi-particles such as excitons created by the absorption of an appropriate photon, and there is a shift in the electron¡Àhole pair ground-state energy to higher values, the so-called blue shift. In their pioneering paper, Efros and Efros (1982) assumed parabolic bands and infinite potential barriers at the surface of a spherical microcrystallite and considered three cases involving R and aB. The Hamiltonian used that governs the envelope function for electrons and holes in the EMA is, as Borrelli et al. (1987) have set down for the general case,   

  

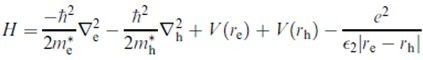
   The equation could be discussed in these 3 regimes:

 

    (a)Weak confinement (R >> a_B, that is R>>a_e; a_h). In this case, only the center of mass motion of the exciton is quantized, while the relative motion of electron and hole are hardly affected. The quantization energy is given, in the above approximations of a spherical dot with infinitely high barriers and neglecting the difference in the dielectric properties of the microcrystallite and the surrounding matrix, by(where M = m_e + m_h is the translationed mass of the exciton.)

 

 

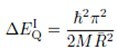
(b)  Medium confinement (ah < R < ae). In this case the motion of the electron is quantized and the hole moves in the potential of the QD and of the space-charge of the electron for the usual situation m_e<<m_h. 

 Continuing to use the above-mentioned approximations, and neglecting the Coulomb energy between electron and hole, one finds

 

 

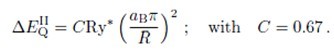
(c) Strong confinement (R<<ae, ah). Since the quantization energy scales with R^-2 and the Coulomb energy with R ^-1 , for this regime one can expect as a first guess

 

 

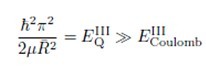
where ¦Ì is the reduced mass of electron and hole. The influence of the Coulomb energy is still partly incorporated, 

 

 

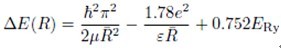
Recently it became obvious that the size of the dots is not the only relevant quantity affecting their linear and especially nonlinear optical properties. The three different growth regimes of the dots which occur during the annealing process of the glasses, namely nucleation, normal growth of the dots and growth through coalescence, result is significantly different properties of, among other things, the interface states between glass matrix and semiconductor dot.

 

Some corrections to EMA:

Effect of surrounding medium

 

The influence of the surrounding medium or matrix of dielectric constant on the energies for the microcrystallites has been considered by Efremov and Pokutnii (1990) and others. They assume parabolic bands for both electrons and holes and worked out the image charges in the matrix for the electrons and holes. 

Finite potential wells in the effective-mass model

It is likely that, for small microcrystallites, the wavefunctions do penetrate the barriers at the interface with the matrix, and the e. ect of using finite potential barriers has been considered by Kayanuma and Momiji (1990), as an extension to the model discussed in the previous section.

  Kayanuma and Momiji consider the case of an electron and hole with coordinates re and rh in a dielectric sphere (1) embedded in a matrix (2), having as conditions for the potentials

 

 

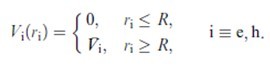
The confining potential V_i satisfies the condition 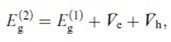,Where E_g⁽²⁾ , the bandgap of the matrix assumed to be glass, has a value of 7eV.

 

Influence of the cluster shape on the quantum size effect

 

Cylindrically shaped microcystallites have been treated by Kayamuma (1991). He again used the EMA with V ~infinite and dealt with Mott¡ÀWannier-type excitons. Cylindrical shapes are thought to occur for PbI₂ and BiI₃ which are layer-structured semiconductors as well as for some types of quantum dot prepared by microfabrication techniques.

 

 

 

 

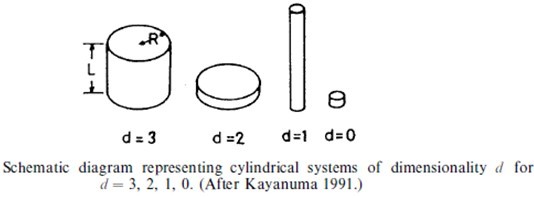
The figure above illustrates some possible shapes, where the dimensionality d depends on the ratios R=L, R=aB and L=aB. Possible limits are as follows.

 

 

 

 

B. Empirical tight-binding method (ETBM).

 

   In their calculations, Wang and Herron (1990, 1991), included non-parabolicity of the energy bands away from the Brillouin zone centre. Lippens and Lannoo (1989, 1990) also used tight binding for the particular case of the II¡ÀVI semiconductors such as CdS and ZnS. They took the valence band to be parabolic but, for the conduction band, non-parabolicity was included by the use of a simple dispersion relation for estimating Ec, and the kinetic energy term for the electrons:

 

 

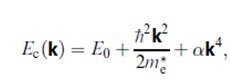
where we see that Ec(k) is expanded to fourth order in k.

 

 

 

 

 

 C.   Empirical pseudo-potential method (EPM).

 

D.   Effective bond order model (EBOM).

 

 Einevoll (1992) determined energy levels for the cubic modifications of the II¡ÀVI semiconductors using this method. The calculations included the EMA and finite potential barriers at the surfaces for the conduction band, and a tight-binding method for the valance bands.

 

E.    Other procedures.

 

There have been several other approaches and improvements in procedures. Nosaka (1991) has developed a very elegant finite-potential-well model, and Que (1992a, b) has given exact solutions for excitons for both spherical crystallites and quantum dots. Sercel and Vahala (1990) used k ¡¡¡¡¨¬¡¡¨¬ p pertubation theory, including non-parabolic bands. Ruppin (1989) used an extended version of Mie light-scattering theory and applied it to the case of weak confinement when R>> aB (see also Masumoto et al.(1991)) and compared his calculations with optical data for CuCl and CdS microcrystallites. Bryant (1988) has treated the extreme case of a quantum well structure, where we finish with an ultra-small quasi-zero-dimensional (quasi-0D) quantum box (flat platelet), and quantum confinement in all three dimensions.

 

        Each of the above models has advantages and limitations. In fact we expect the EMA and EBOM to overestimate confinement energies, but the ETBM to give an nderestimate. We also recognize that all the methods can break down for the very smallest clusters, say R<1nm , because of possible surface effects and structural changes.