Temperature Dependence

Fluctuation of μ with Temperature

The temperate dependence of μ is dominated by two factors; phonon scattering and ionized impurity scattering. As temperature increases, thermal vibrations (phonons) within a semiconductor increase and cause increased scattering. This results in a decrease in the carrier mobility. We know that

$\mu=\frac{e}{m}\tau$

where tau is the mean free time between collisions. The mean free path may be written as proportional to

$l\sim\tau T^{\frac{1}{2}}$

Now consider that the mean free path is inversely proportional to the scattering probability, and that the scatting probability may be taken to be proportional to the energy of the lattice (i.e. to T). This allows tau to be written as

$\tau_{thermal}\sim lT^{-1/2}\sim T^{-3/2}$

We therefore expect this decrease in the mobility to be proportional to T^-3/2.

The effect of ionized impurity scattering, however, decreases with increasing temperature due to the average thermal speeds of the carriers being higher. The carriers spend less time near an ionized impurity as they pass and the scattering effect is thus reduced. This is modelled by assuming that no scattering will occur unless the electron is close enough to the ion for the electrostatic energy to be comparable with the thermal energy.

$\frac{Ze^{2}}{4\pi\epsilon r_{s}}=\frac{3}{2}}kT$

which yields a radius

$r_{s}=\frac{Ze^2}{6\pi\epsilon kT}$ .

Next, we can argue that the scattering power of the ion may be represented by a scattering cross-section

$S_{s}=r_{s}^2\pi=\frac{1}{\pi}\left(\frac{Ze^2}{6\epsilon kT}\right)^2$ .

Finally, assuming that the mean free path is inversely proportional to the scattering cross-section, we obtain the relationship

$\tau_{ionized impurity}=lT^{-1/2}\sim S_{s}^{-1}T^{-1/2}\sim T^{+3/2}$ .

Therefore we can expect the mobility due to ionized impurity scattering to increase as temperature rises according to T^+3/2.

These two effects operate simultaneously, with the total collision time equalling

$\frac{1}{\tau}=\frac{1}{\tau_{thermal}}+\frac{1}{\tau_{ionized impurity}}$

In general, ionized impurity scattering dominates at low temperatures, whilst at higher temperatures, phonon scattering dominates. Experimental values of the temperature dependence of the mobility in Si, Ge and GaAs are listed in table below [1].

	Si	Ge	GaAs
Electron Mobility	T^-2.4	T^-1.7	T^-1.0
Hole Mobikity	T^-2.2	T^-2.3	T^-2.1

The Affect of Temperature on V_H

In order to understand how Hall voltage changes with temperature, we must first consider the conductivity of the sample being measured. The electrical conductivity of a semiconductor can be expressed in the following way:

$\sigma=\left(N_{e}(T)\mu_{e}(T)+N_{h}(T)\mu_{h}(T)\right)e$

Note that both the carrier concentrations (N_e and N_h) and the mobilities depend on temperature, though with different functional forms.

In the extrinsic temperature range, where T is only large enough to ionise any donors within the semiconductor, the carrier concentrations remain constant and the only change in sigma with temperature results from the change in the mobilities. Assuming phonon scattering dominates, we know μ varies as T^-3/2. Thus we know σ~T^-3/2, and given that σ=1/ρ and ρ∝R we can determine that R~T^3/2.

As stated previously, the Hall voltage can be written as

$V_{H}=-\frac{IB}{dne}$

with only the current being temperature dependent. This current, I, may be written in the form

$I=\frac{V}{R}$

which implies that I, and thus V_H vary according to T^3/2. In reality, these fluctuations with temperature are quite small and V_H may in practice be considered constant in the extrinsic regime.

In the intrinsic region in which the temperature is high enough to excite charge carriers up from the valence band into the conduction band, the carrier concentrations (N_e and N_h) increase exponentially with T. This dominates any mobility affects on the electrical conductance and results in a rapid decrease in the resistivity of the semiconductor with increasing temperature. Thus the Hall voltage falls as T increases.

Determining the Energy Gap

The variation of conductivity with temperature also allows us to measure the energy gap between the valence and conduction bands. Again the conductance of a semiconductor is

$\sigma=\left(N_{e}\mu_{e}+N_{h}\mu_{h}\right)e$

For an intrinsic material, we know that

$N_{e}=N_{h}=constant*T^{\frac{3}{2}}exp\left(\frac{-E_{g}}{2kT}\right)$

Combing these two equations yields

$\sigma=constant*e(\mu_{e}+\mu_{h})T^{\frac{3}{2}}exp\left(\frac{-E_{g}}{2kT}\right)$

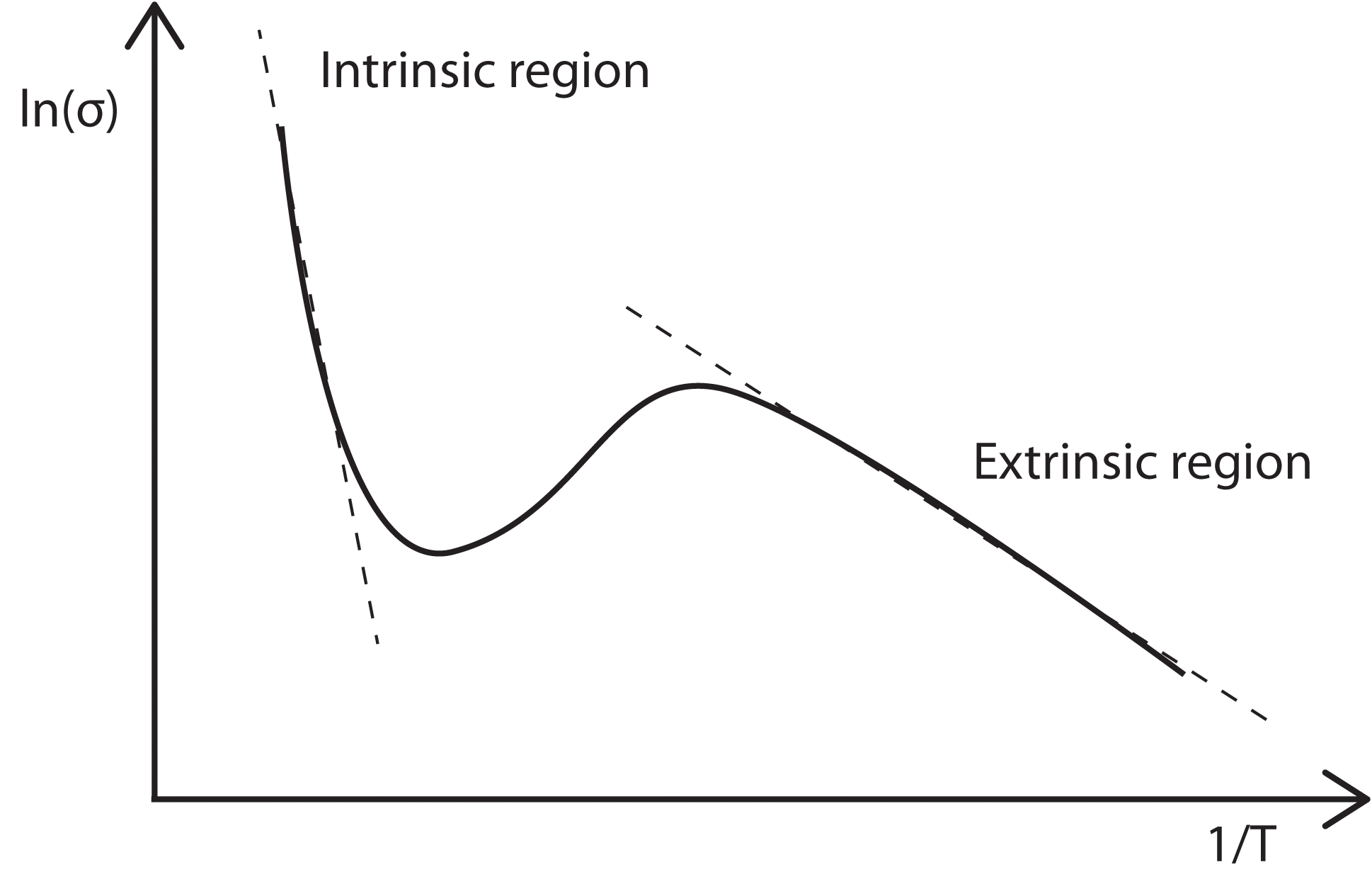
We can once again ignore the T^3/2 variation, which will be mostly negligible compared with the exponential temperature variation. Thus a plot of ln(σ) vs 1/T will have a slope of –Eg/2k, which yields a value for Eg.

In the case of doped semiconductors, we note that at high temperatures they are intrinsic in behaviour and become pseudo-intrinsic at low temperature, with and energy gap equal to the gap between the impurity level and the band edge. Therefore on a plot similar to the one mentioned above we would expect two straight-line regions with different slopes. In the region between these slopes the temperature is high enough to ionize the donors fully but not high enough to ionize an appreciable number of electrons from the lattice. Hence, in this temperature rage the carrier density will not be greatly influenced by temperature and the in mobility that were previously neglected will determined the shape of the curve.

sigma(T)

References

Bart van Zeghbroeck, Principles of Semiconductor Devices, Boulder, 2006

Fluctuation of μ with Temperature

The Affect of Temperature on VH

Determining the Energy Gap

References

The Affect of Temperature on V_H