Ultrasound for materials characterisation
Ultrasound also has uses in characterising materials. Two examples are given here; vibrational analysis for measuring the properties of semiconductor membranes, and low temperature measurements of the elastic constants and magnetic phase of new single crystal materials.
Vibrational analysis of membrane structures
Microelectromechanical systems (MEMS) are becoming more important in technology. The Nano-Silicon group is developing suspended structures of new materials for applications [1]. There is a risk of damage to MEMS during production or in use. To characterise the properties, such as the presence of damage or measure the residual stress, the vibrations of the membrane in the ultrasound frequency range can be studied [2,3]. A membrane will have resonant modes labelled by n and m which satisfy the equation
for a rectangular membrane of side lengths Lx and Ly, when measured in vacuum.
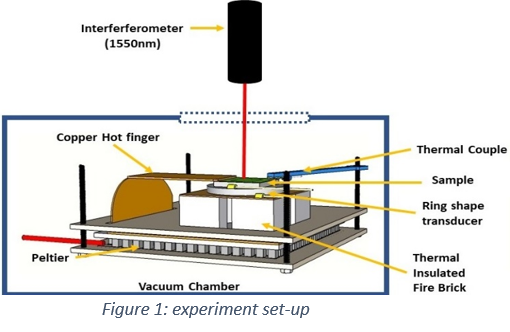
Figure 1 shows the measurement set-up. The membranes are vibrated using a piezoelectric transducer, and vibrations are mapped during a two-dimensional scan using a laser interferometer. The pressure can be controlled using a vacuum chamber, and a heating/cooling stage can be used to study the temperature dependence of the material behaviour.
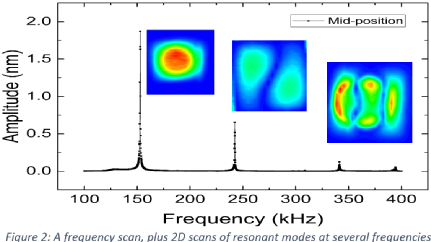
Figure 2 shows a frequency scan done on a membrane to identify different resonant modes. As the vibration amplitude is increased, the vibrational behaviour changes, and non-linear behaviour can be observed [3].

The videos show the behaviour of a 3C-SiC membrane on a Si substrate vibrated at low pressure at a frequency of 206.2 kHz. The first video shows the behaviour measured experimentally for a sinusoidally oscillation voltage with a peak of 0.1 V applied to the piezoelectric transducer for the 1:3 mode; this shows linear vibrations of small amplitude. When the peak voltage is increased to 8.3 V the behaviour is shown in the second video.
Low temperature measurements of single crystals
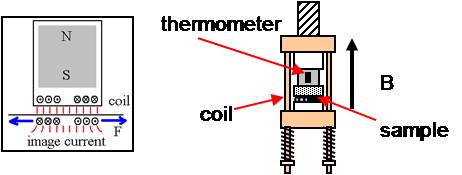
Measurements of the fundamental properties of single crystals, such as identifying phase changes and measuring the elastic constants, can be done by analysing ultrasound echoes. The ultrasonic velocity within the material can be calculated from the time spacing between echoes, for propagation of longitudinal or shear waves in different crystallographic directions.
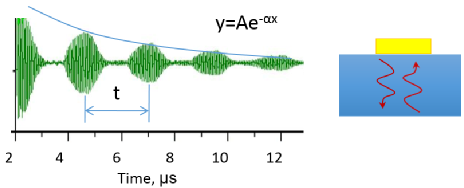
The calculated velocity can then be used to calculate elastic constants. In the above sample, Gd64Sc36, for longitudinal waves generated along the crystal c-axis, the elastic constant which is measured is C33= ρv2. The elastic constants can change as, for example, the temperature of the material, or the magnetic field in which it sits, is changed. At a phase transition the elastic constants soften and the attenuation of the sound waves typically increases.
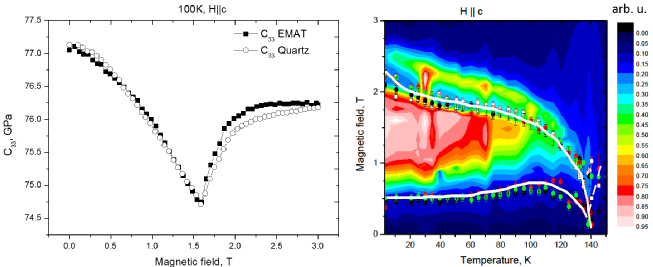
C33 as a function of magnetic field, measured at 100K, is shown above. Measurements of phase changes using C33 and attenuation are shown as points [4].
Standard measurements use contact transducers, such as quartz, to generate and detect ultrasound. We are developing EMAT techniques to remove the need for couplant. In NDT, the required magnetic field is provided by a permanent magnet; however, here we have a superconducting magnet which is used to generate a magnetic field to change the sample properties. The colour scale on the image above is a measure of the EMAT efficiency during measurements, and also shows the phase transition behaviour.
- V.A. Shah, M. Myronov, S.D. Rhead, J.E. Halpin, A. Shchepetov, M.J. Prest, M. Prunnila, T.E. Whall, E.H.C. Parker and D.R. Leadley, "Flat single crystal Ge membranes for sensors and opto-electronic integrated circuitry," Solid State Electronics (2014) 98, 93-98
- O. Trushkevych, V.A. Shah, M. Myronov, J.E. Halpin, S.D. Rhead, M.J. Prest, D.R. Leadley and R.E. Edwards, “Laser-vibrometric ultrasonic characterization of resonant modes and quality factors of Ge membranes”, Science and Technology of Advanced Materials, 15, 2, 025004 (2014)
- L. Q. Zhou, G. Colston, M. J. Pearce, R. G. Prince, M. Myronov, D. R. Leadley, O. Trushkevych, and R. S. Edwards, "Non-linear vibrational response of Ge and SiC membranes," Applied Physics Letters, vol.111 (2017) 011904
- O. Trushkevych, Y. Fan, R. Perry and R.E. Edwards “Magnetic phase transitions in Gd64Sc36 measured using noncontact ultrasonics”, Journal of Physics D: Applied Physics, 46, 105005 (2013)
