Research Projects
This page contains some project outlines and associated graphics. It is intended to be a resource for students and colleagues wanting to see what we are or have been working on recently. We normally place new content here at the top of the list when we have gained some confidence in the projects feasibility. If time permits, we also add some publication outcomes later. But then the aim of the project might already have shifted somewhat.
Lieb models and their extensions
Jie Liu, Carlo Danieli, R. A. Römer
| Uncorrelated disorder in generalized 3D Lieb models gives rise to the existence of bounded mobility edges, destroys the macroscopic degeneracy of the flat bands and breaks their compactly-localized states. We now introduce a mix of order and disorder such that this degeneracy remains and the compactly-localized states are preserved. We obtain the energy-disorder phase diagrams and identify mobility edges. Intriguingly, for large disorder the survival of the compactly-localized states induces the existence of delocalized eigenstates close to the original flat band energies -- yielding seemingly divergent mobility edges. For small disorder, however, a change from extended to localized behavior can be found upon decreasing disorder -- leading to an unconventional ``inverse Anderson" behavior. We show that transfer matrix methods, computing the localization lengths, as well as sparse-matrix diagonalization, using spectral gap-ratio energy-level statistics, are in excellent quantitative agreement. The preservation of the compactly-localized states even in the presence of this disorder might be useful for envisaged storage applications. |
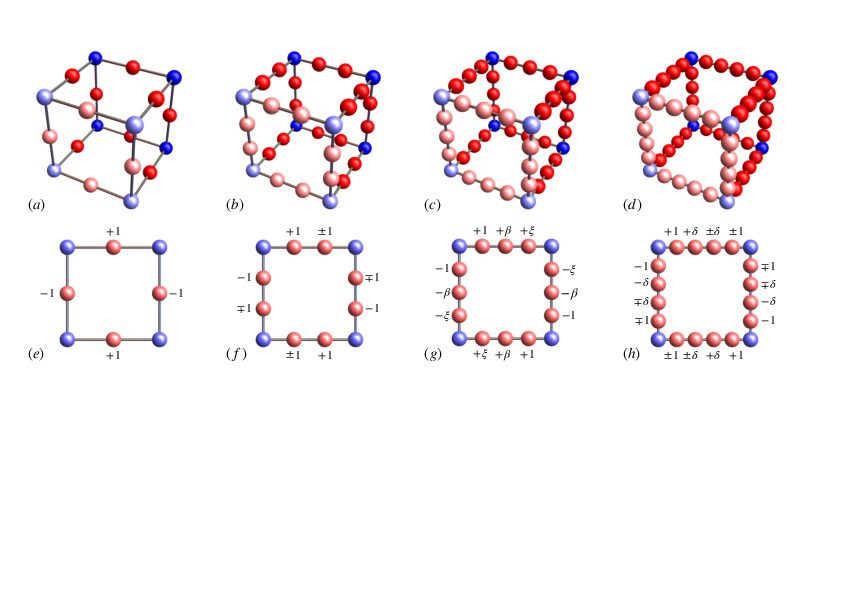
Schematics of various extended Lieb models.
|
Topological phases in 3D
Syl (Nathan) Shaw, R. A. Römer
| Topological phase transitions have long been an exciting area of study. Like topological phases themselves, the transitions from one topological phase to another are usually not governed by ideas of broken symmetry. Instead, a topological index abruptly changes at a topological phase boundary. The best studied example involves integer quantum Hall transitions, where previously renormalization group (RG) studies have played an important role to ascertain the universal properties of the transition. A recent generalization of scattering-type models to 3D topological systems now suggests that such RG approaches should also be possible in 3D. This is what the work intends to find out. |
 |
Novel approaches to interacting and disordered systems
Yilun Gao, R. A. Römer
| Disordered quantum systems continue to play a key role in theoretical developments of modern condensed matter physics. Originally, this is due to Anderson’s realization in 1958 that the quantum wave nature of condensed matter can lead to interference effects that suppress the classically expected charge transport mechanisms – the birth of Anderson localization. Already in Anderson’s paper, it was discussed how the situation might be influenced by many-body effects. In the last decade, following the increase in computational power to allow the construction of meaningfully large Hilbert spaces even for interacting systems, this interplay of disorder and many-body physics has received much attention but remains restricted to small system sizes. What really is needed is a novel approach at solving the underlying Schrödinger equations. Recently, machine learning and deep learning have emerged as numerical techniques that use strategies of artificial intelligence to predict outcomes of numerical experiments. It therefore seems possible to use DL techniques to speed up such sparse matrix codes to construct well-approximated eigenstates for very large system size. |
|
Machine learning the Anderson transition
Quangminh Bui-le, R. A. Römer
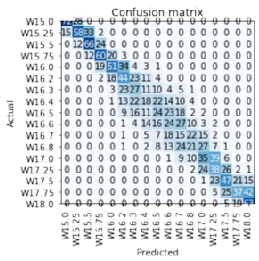
| Machine learning and deep learning are statistical analysis techniques that use strategies of artificial intelligence to characterize complex data and extract deep information. In recent years, these techniques have begun to be used not only in traditional computer science test cases, but also in real world applications as well as, more recently, in areas of advanced physics. In this researcht, we want to use these methods to a) identify, characterize and classify the metal-insulator transition in the two- and three-dimensional Anderson model of localization and b) develop appropriate version of “scaling” applicable to machine+deep learning techniques. |
Confusion matrix for 17 disorder "classes" around the Anderson transition. |
Flexibility of SARS-CoV-2-related protein structures
N. S. Römer, A. K. Wallis, R. A. Römer
| We are using in silico modelling of SARS-CoV-2 drug targets, i.e. SARS-CoV-2 protein structures as deposited on the Protein Databank (https://www.rcsb.org/), to study the flexibility, rigidity and mobility of said proteins. This is generally an important step in trying to ascertain the dynamics of proteins for further drug-related docking studies (where people usually see if certain molecules, such as antivirals, can attach/dock to said proteins and hence interrupt their usual working). Usually, state-of-the-art molecular dynamics studies of protein dynamics can take weeks and months, our method only takes minutes to hours. Although the physical/biological basis for the method is less sophisticated, the results should be able to offer a good first guess on the possible protein dynamics and hence allow to circumvent lengthy MD studies. Due to the speed of the method, large-scale screening (of all thus far published SARS-CoV-2 protein structures in the PDB!) is possible. |
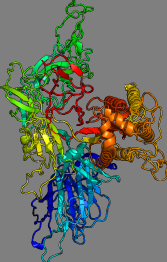
The SARS-CoV-2 "spike" protein, the opener of human cells.
|
Machine learning phases and phase transitions
Djenabou Bayo, R. A. Römer
| One of the central challenges in condensed matter physics is to understand how different phases of matter can arise and how these phases can be characterized. A most simple example is of course provided by the three states of water, i.e. solid ice, liquid water and gaseous vapor. These three phases are distinguished from another by well-defined transitions. In the quantum realm, such phase transition exists as well and give rise to many properties of the world in which we live. Phenomena such as, e.g., magnetism and superconductivity are prime examples which are well known. In recent years, other, so-called quantum phase transitions, have been added to the zoo of transitions. One such example, disorder-induced localisation embodies the paradigmatic example of a quantum phase transition, i.e. driven by the quantum wave-like nature of matter. Conventionally, the study of phase transitions is tedious because right at the transition, fluctuations from equilibrium dominate, making analytic and numeric treatments challenging. Recent advances in machine learning (ML) and deep learning (DL) promise to offer an alternative route to studying such transitions. The ML/DL approach seems to be able to detect phases and transitions between them directly from the computed quantum states. The states are treated similar to classical “images” where early neural network approaches had already shown to be effective in detecting and extracting information. During the fellowship, I intend to study the application of ML/DL approaches to phases in disordered quantum systems at equilibrium, i.e. Anderson transitions, and non-equilibrium interacting quantum systems after a quench, i.e. DQPTs. Both supervised and unsupervised learning will be applied in both cases. |
Test percolation states to check whether the CNN can find the presence of a spanning cluster, or, indeed, its absence. |
Dynamical quantum phase transitions in spin chains
Leonardo Benini, R. A. Römer
| We study dynamical properties of many-body localized systems through the lens of dynamical quantum phase transitions (DQPTs) theory. We explore the quench dynamics of a one-dimensional Heisenberg model with quasi-periodic on-site magnetic fields, investigating the emergence of singularities in the return rate of the Loschmidt echo in the strong MBL regime. Quenching from an initially ordered Neel state, we show the appearance of a sequence of DQPTs deep in the MBL phase, periodically distributed along the real-time axis. We then establish a connection between this out-of-equilibrium non-analytic behavior of the dynamical free energy and the oscillations of a well-known sensitive measure of memory effects in MBL systems, i.e. the imbalance. Our quantum quench protocols can be effectively realized in ultra-cold atoms setups, exploiting recently established quantum many-body interferometry techniques. |
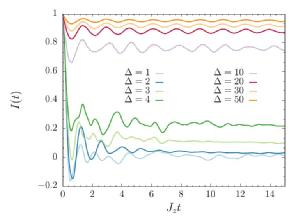
The imbalance as a function of (rescaled) time for different disorder strength after a quantum quench from the Neel state.
|
PDB2Movie protein flexibility and dynamics server
Sam Moffat, R. A. Römer
| Protein function frequently involves conformational changes with large amplitude on timescales which are difficult and computationally expensive to access using molecular dynamics. In this project, we combine three computationally inexpensive simulation methods, (i) normal mode analysis using the elastic network model, (ii) rigidity analysis using the pebble game algorithm, and (iii) geometric simulation of protein motion, to explore conformational change along normal mode eigenvectors. The web server at PDB2Movie allows for easy submission and retrieval of such computations. |
 |
|
|
Strongly correlated quantum many-body systems
Xiwen Guan, R. A. Römer
| One of the central challenges in condensed matter physics is to understand how different phases of matter can arise and how these phases can be characterized. Many phenomena such as, e.g., superconductivity, magnetism and quantum phase transitions in strongly correlated systems, Bose-Einstein condensation of dilute gases and of excitons in semiconductors, electronic transport in low-dimensional systems and heavy-fermion physics, are known to exist due to the collective nature of the underlying many-body processes. Collective phenomena are particularly strong in low-dimensional systems where the reduced dimensionality enhances the interaction of elementary constituents. |
|
| "High order local and nonlocal correlations for 1D strongly interacting Bose gas", EJKP Nandani, R. A. Römer, S. Tan, X.-W. Guan, New J. Phys. 18, 055014 (2016) |
|
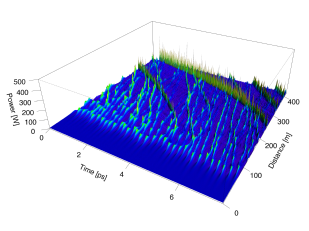
Rogue waves
M. Eberhard, R. A. Römer, A. Savojardo
| We are using the non-linear Schrödinger equation (NLSE) to model the transmission statistics for wave pulses in next generation fibre optic based communication systems. We have first developed and applied a massively parallel simulation code for such systems on the UK's national high-performance computing systems HECToR/ARCHER and the BlueGene of the Hartree Centre. We have shown linear scaling up to 100k cores. The algorithm hops forward and backward between time and frequency domain to propagate the signal along the fibre using high-performance Fourier techniques. This allows for very small step sizes of 10-100 m for system lengths equal to the distances between continents (transatlantic 6,000 km, transpacific 10,000 km). This means on the order of 6*104 to 106 forward and backward Fourier transformations per simulation run. In order to avoid those, in principle, huge numerical Fourier transforms, we use the Overlap-Add method to break the problem down into a set of overlapping blocks. A copy of the code is available at GitHubLink opens in a new window. The numerical strategy has allowed us to get unprecedented accuracy and statistics to observe the emergence of non-linear effects such as the generation of rogue waves. These rogue waves have detrimental effects on the optical systems - leading to overload and burnout --- but are of course part of the much larger phenomenon of rogue waves in general. We are currently extending our studies to the variants of the Korteweg de Vries equation to see if the mechanisms identified for the emergence of the rogue waves in the NLSE is general. Already you can look at a talk and also a Hartree Centre Case Study. |
|
Digital precession electron diffraction – nanoscale structure solution
R. Beanland, Keith Evans, Alex Hubert, R. A. Römer
| The aim of this project is to revolutionise structure solution at the nanoscale in electron diffraction through the invention and implementation of a new technique, Digital Precession Electron Diffraction (D-PED). This technique will allow the collection of single-crystal like structure factors from nm-scale homogeneous regions of highly inhomogeneous samples such as multiferroic materials containing ferroelastic, ferroelectric and magnetic domains, nano-composites, alloys etc. This will lead to the capacity to undertake true structural studies within individual domains or nano-regions of complex functional materials that are presently too challenging for all but a few specialists. In particular, the methodology that we envisage here will actually make structure determination on the nanoscale accessible in a routine fashion, via a relatively inexpensive addition to the typical modern electron microscope. Project software: We are working on a code to simulate the images shown here. The code is called Felix since it uses the traditional wave vector method pioneered by Felix Bloch. You can get a copy of the code from GitHub. |
|
The interplay of mutations and electronic properties in disease-related genes
R. A. Römer, S.A. Wells
| We have discovered that cancer-causing genetic mutations have better-disguised electronic signatures than other mutations - a trait which could help them fly under the radar of the body’s defence mechanisms. Results of a our study hint at the possibility that one day the electronic properties of DNA could play a role in early diagnosis and detection of mutation hotspots. In the work, we modelled every possible mutation for 162 disease-related genes, a total of 5 billion calculations. When they compared the models with medical databases of real-life mutations known to have caused cancer in individuals, we found that the real-life mutations had a “stealthier” electronic structure than the theoretical mutations which didn’t have a documented real-life counterpart. These disease-causing mutations caused a smaller change in the electronic structure of the DNA molecule, which may make them less detectable to the cell’s damage repair process at work on a molecular level . |
|
| "The interplay of mutations and electronic properties in disease-related genes", C.-T. Shih, S. A. Wells, C.-L. Hsu, Y.-Y. Cheng and R. A. Römer, Scientific Reports 2, 272-9 (2012), Warwick press release, Tunghai press release, audio |
|
Quantum states of interacting particles in nano-rings
A. M. Fischer, R. A. Römer
| We study analytically the optical properties of a simple model for an electron-hole pair on a ring subjected to perpendicular magnetic flux and in-plane electric field. We show how to tune this excitonic system from optically active to optically dark as a function of these external fields. Our results offer a simple mechanism for exciton storage and readout. Currently, we are extending this model to include higher-dimensional effects. |
|
Ripples in chemically modified graphene
N. R. Wilson, G. Rowlands, R. A. Römer
| The mechanical, electrical and chemical properties of chemically modified graphene (CMG) are intrinsically linked to its structure. Here we study the topographic structure of free-standing CMG using atomic force microscopy and electron diffraction. We find that, unlike graphene, suspended sheets of CMG are corrugated and distorted on nanometre length scales. AFM reveals not only long range (100 nm) distortions induced by the support, as previously observed for graphene, but also short-range corrugations with length scales down to the resolution limit of 10 nm. These corrugations are static not dynamic, and are significantly diminished on CMG supported on atomically smooth substrates. Evidence for even shorter range distortions, down to a few nanometres or less, is found by electron diffraction of suspended CMG. Comparison of the experimental data with simulations reveals that the mean atomic displacement from the nominal lattice position is of order 10% of the carbon-carbon bond length. Taken together, these results suggest a complex structure for chemically modified graphene where heterogeneous functionalisation creates local strain and distortion. |
Collective excitations of doped graphene in a strong perpendicular magnetic field
A.M. Fischer, R. A. Römer /A.B. Dzyubenko
| As the building block for many other carbon-based structures, graphene is a material of fundamental importance. It can be thought of as a single layer of graphite or more precisely as a two-dimensional array of sp2-bonded carbon atoms forming a honeycomb lattice. Since it was first isolated experimentally in 2004, it has been the subject of an intense research effort. We consider a single layer of graphene in a strong perpendicular magnetic field. The aim is to determine the collective (many-body) excitations of the system, which become localised in the presence of a low density of impurities. This low impurity density limit is pertinent, since graphene is a naturally clean system. The excitations are collective in the sense that infinitely many single particle (electron-hole) excitations are strongly mixed by the Coulomb interaction. The model uses a single axially symmetric impurity potential and builds up an excitonic wavefunction from a single particle basis. The wavefunction amplitudes and energy eigenvalues are obtained by diagonalising a secondary quantised Hamiltonian, which treats both the impurity-electron interaction and the electron-electron interactions beyond the mean field level. Having obtained some interesting results and symmetries for a long-range Coulomb impurity, we are now examining the case of a delta function impurity, due to e.g. a neutral foreign atom. The latter case, whilst easier in some respects, provides different challenges such as the need to consider scattering between the two valleys in graphene and the resulting mixing of excitations with different orbital angular momentum projections, Mz. |
|
Protein rigidity analysis and normal modes of motion
S.A.Wells, J.E. Jimenez-Roldan, R. A. Römer /R. Freedman
| Disease associated with misfolded proteins leading to accumulation of amorphous protein in vital organs can induce conditions such as Alzheimer’s, Hungtington’s or Parkinson’s disease. Protein rigidity analysis arises from studies on glassy networks and it is a promising technique to study protein rigidity distribution and protein folding. We use X-ray crystal structures from the Protein Data Bank to obtain the atoms positions and apply protein rigidity analysis using the software FIRST to determine the flexible and rigid parts of the molecule at different energy cut off. Further, we also determine the directions in which different parts of the protein are able to move, run simulations and hence we can guide experiments, test predictions and gain useful information to understand the folding process and protein motion. Following our latest paper on protein rigidity across protein families we are now focusing on the folding pathway for BPTI and predicting the normal modes of motions of Disulphide Isomerase, and in designing experiments to test our predictions. This project is a collaboration with R. Freedman at University of Warwick, Biological Sciences. |
![Three dimensional representation of rigidity distribution for Trypsin protease at energy cut off E=2 Kcal/mol. [Image: Three dimensional representation of rigidity distribution for Trypsin protease at energy cut off E=2Kcal/mol.]](trip_e2.png)
Three dimensional representation of rigidity distribution for Trypsin protease at energy cut off E=2 Kcal/mol. Thick lines represent rigid regions. |
| "Comparative analysis of rigidity across protein families", S.A. Wells, J.E. Jimenez-Roldan, R. A. Römer, arXiv:0905.4232 (2009) [PDF] |
|
The application of multigrid methods to the Helmholtz/Anderson problem
S. M. Mallion, R. A. Römer / P. Plechac
| The similarities of the Helmholtz equation to the Schrödinger equation make it an ideal testing ground for programs designed to solve the latter. Multigrid methods are one way of solving the superficially similar Laplace equation and they can be highly efficient and easily adaptable to the specifics of an individual problem. The very nature of the multigrid process however, with its repeated interpolation and smoothing steps prevents it from converging to rapidly oscillating solutions such as those occurring with the Helmholtz equation. This is particularly problematic when the diagonal term includes randomness - the Anderson model. We propose the use of the comparatively slower varying WKB ansatz as an assumed form for the solution to the Helmholtz equation. This, with appropriately set of re-derived discrete differential operators, has the potential to negate the inherent problems of the Laplacian multigrid solver and allows convergence even to the highly oscillating solutions of the Helmholtz equation. |
Scale-free disorder in the Anderson model of localization
M. L. Ndawana, R. A. Römer / M. Schreiber
| The successful analysis of the metal-insulator transition (MIT) in the Anderson model of localization has hitherto been limited to short-range or uncorrelated diagonal disorder. In this Letter we report the effects of long-range power-law correlated disorder - so called scale-free disorder - on the MIT. Scale-free disorder is omnipresent in nature. It is found in many diverse situations in biological and in physical systems, in city growth patterns and in economics. The effects of scale-free disorder on the critical properties of physical systems have recently received much renewed attention. Of particular interest to us is the influence of scale-free disorder in the neighborhood of an MIT when the localization length becomes sufficiently large. Scale-free disorder can affect the character of the divergence as shown previously for the classical percolation problem. Therefore it appears to be possible that the criterion based on potential fluctuations can be applied also to quantum phase transitions such as the Anderson-type MIT, where the critical exponent of the localization lengths is determined from the divergence of the quantum-localization length at the critical point. It is the purpose of this project to investigate this possibility |
![Critical exponent v of the metal-insulator transition as a function of the correlation strength exponent alpha [Image: Critical exponent v of the metal-insulator transition as a function of the correlation strength exponent alpha]](../images/colfig-nu_e.png)
Critical exponent v of the metal-insulator transition as a function of the correlation strength exponent alpha |
| "The Anderson Metal-Insulator Transition in the Presence of Scale-Free Disorder", M. L. Ndawana, R. A. Römer, M. Schreiber, Europhys. Lett. 68, 678-684 (2004). [gzipped Postscript, PDF] |
|
Interacting particles and disorder
C. Sohrmann, R. A. Römer
| The role played by many-particle interactions is much less understood. Even for disordered quantum many-body systems in 1D, no entirely consistent picture exists. Renormalization group arguments together with the bosonization technique suggest that the ground states belong to strongly localized phases. Nevertheless, depending on the type of interaction and on the basic symmetries of the many-body wave functions, transport properties in the ground state may be enhanced. Even less is known about the interplay of interaction and disorder in 2D, where many of the analytical techniques used in 1D are not applicable and numerical approaches are limited to much smaller system sizes. Thus recent experimental results, which indicate the existence of an MIT in certain 2D electron gases at B=0, are a challenge to our current understanding. In the samples considered, the Coulomb interaction is estimated to be much larger than the Fermi energy and so the observed MIT may be due to an interaction-driven enhancement of the conductivity. A recent reevaluation of the principles of scaling theory shows that these experimental results do in fact not violate general scaling principles. However, it is not yet clear that this transition does indeed correspond to an MIT since other recent arguments suggest that the transition might be understood as an insulator-superconductor transition. |
![Compressibility of an interacting (HF) 2DEG as function of density and magnetic field [Image: Compressibility of an interacting (HF) 2DEG as function of density and magnetic field]](../images/qh-compress-tmb.png)
Compressibility of an interacting (HF) 2DEG as function of density and magnetic field |
Electronic transport in DNA - the disorder perspective
D. Klotsa, R.A. Römer / M.S. Turner, P. Taylor
| The question on whether DNA can conduct electricity, and if so how this can be utilized, has been a subject of discussion particularly since direct experimental results became available. Part of the motivation for such studies is the potential use of DNA in nanotechnology and also the possibility of DNA damage-repair mechanisms via electron transfer. Despite the enhanced activity in both experimental and theoretical studies, the complexity of DNA is still preventing us from forming a consistent understanding. In most models it has been assumed that electronic transport takes place along the long axis of the DNA molecule and that the conduction path is due to p-orbital overlap between consecutive bases; densityfunctional calculations have shown that the bases, especially Guanine, are rich in p-orbitals. Quantum mechanical approaches to the problem use standard onedimensional (1D) tight-binding models. Of particular interest to us is a 1D model which includes the backbone structure of DNA explicitly and exhibits a semiconducting gap. |
![Increasing localization lengths with increasing backbone disorder for the ladder model of DNA [Image: Increasing localization lengths with increasing backbone disorder for the ladder model of DNA]](../images/dna-bb.png)
Increasing localization lengths with increasing backbone disorder for the ladder model of DNA |
| "Electronic Transport in DNA", K. D. Klotsa, R. A. Römer, M. Turner, Biophys. J. 89, 2187-2198 (2005). [gzipped Postscript, PDF] |
|
Thermoelectric transport at the MIT
A. Croy, R.A. Römer / A. MacKinnon
The Anderson model of localization and the so-called disorder driven metal-insulator transition (MIT) in 3D has been subject of intense study for the last 45 years. Using analytical and numerical methods, the form of the density of states, the energy and disorder dependence of the localization lengths as well as the spatial distribution of its eigenstates and the critical behavior at the transition were determined. However, thermoelectric properties, such as thermopower and thermal conductivity, have been relatively neglected. The calculations of these properties are usually based on the Chester-Tellung-Kubo-Greenwood (CTKG) formalism and perturbative methods are used to obtain low and high temperature limits. These methods are macroscopic since they rely on the explicit, phenomenological form of the conductivity. It is the purpose of this project to investigate the thermoelectric properties of disordered systems at the MIT using an extension to the recursive Green's function method (RGFM), which does not depend on any assumptions about the explicit form of the conductivity and is therefore a microscopic method. In particular we hope to support the sign change of the thermopower in non-crystalline systems, which is commonly observed at low temperatures although the majority charge remains unaffected. Another interesting question concerns the validity of the empirical law of Wiedemann-Franz for metals, which states that the quotient of thermal and electric conductivity is proportional to the temperature.
Solitons in non-linear PDEs
J. He, R.A. Römer /
| We present a systematic way to construct solutions of the (n=5)-reduction of the BKP and CKP hierarchies from the general tau function of the KP hierarchy. We obtain the one-soliton, two-soliton, and periodic solution for the bi-directional Sawada-Kotera (bSK), the bi-directional Kaup-Kupershmidt (bKK) and also the bi-directional Satsuma-Hirota (bSH) equation. Different solutions such as left- and right-going solitons are classified according to the symmetries of the 5th roots of exp(i epsilon). Furthermore, we show that the soliton solutions of the n-reduction of the BKP and CKP hierarchies with n= 2 j +1, j=1, 2, 3, ..., can propagate along j directions in the 1+1 space-time domain. Each such direction corresponds to one symmetric distribution of the nth roots of exp(i epsilon). Based on this classification, we detail the existence of two-peak solitons of the n-reduction from the Grammian tau function of the sub-hierarchies BKP and CKP. If n is even, we again find two-peak solitons. Last, we obtain the "stationary" soliton for the higher-order KP hierarchy. |
![Collision of left and right going solitons [Image: Collision of left and right going solitons]](../images/kp-bw-bsk2leftright.png)
Collision of left and right going solitons |
| "Solving bi-directional soliton equations in the KP hierarchy by gauge transformation", J. He, Y. Cheng, R. A. Römer, J. High Energy Phys. 03, 103-37 (2006). [gzipped Postscript, PDF] | |
The local density of states in disordered systems
J. Stephany, R.A. Römer / M. Morgenstern
| The potential landscape for a 2D disordered electron system obtained by depositing Fe atoms on the InAs(110) surface has been determined experimentally by scanning-tunneling spectroscopy. We use this potential as the input to compute the local density of states of this system by a direct diagonalization of the associated Anderson localization hamiltonian using a modified Lanczos algorithm. The result is then compared with the experimental local density of states obtained by scanning tunneling spectroscopy. We next perform the correspondig computation for the case in which an external magnetic field is applied where Landau quantization has been recently observed. |
![LDOS of Landau levels [Image: LDOS of Landau levels]](qhe-ldos.jpeg)
Local density of states of Landau levels at different Fermi energies |
| "The Quantum Hall transition in real space: From localized to extended states", K. Hashimoto, C. Sohrmann, J. Wiebe, T. Inaoka, F. Meier, Y. Hirayama, R. A. Römer, R. Wiesendanger, and M. Morgenstern Phys. Rev. Lett. 101, 256802-4 (2008). [PDF] | |
Quantum transport in a strong magnetic field
P. Cain, R. A. Römer / M. E. Raikh
| In 1980 von Klitzing et al. showed that in certain 2D materials subject to a perpendicular magnetic field distinct steps - multiples of h/e2 - in the Hall resistance appear when measured as a function of the gate voltage. These steps are accompanied by simultaneous peaks in the conductivity measured along the samples suggesting that discrete parts of the electronic spectrum become delocalized. Since then much effort has been dedicated towards the understanding of this "quantum Hall-effect" (QHE). The disorder present in the samples plays a crucial role in the QHE. In particular, the integer QHE can be explained, at least qualitatively, by a variant of the Anderson model in 2D at finite magnetic field. We are currently investigating whether the assumption of a macroscopically, i.e., scale-invariant, correlated disorder potential can change the value of the critical exponent observed at the QH transition. This research has been triggered by apparent observed deviations from scaling. Our approach is a combination of analytical and numerical RG, pioneered by Prof. M. E. Raikh (Salt Lake City) with whom we collaborate. |
![Building a super-saddle point out of 5 saddle points - the heart of the RG [Image: Building a super-saddle point out of 5 saddle points - the heart of the RG]](../images/qhrg-5sp-tmb.png)
Building a super-saddle point out of 5 saddle points - the heart of the RG |
| "Real-space renormalization-group approach to the integer quantum Hall effect", P. Cain, R. A. Römer, Int. J. Mod. Phys. B 19, 2085-2119 (2005). [gzipped Postscript, PDF] |
|










![WKB-type smoothers versus weighted-Jacobi and Gauss-Seidel smoothers [Image: WKB-type smoothers versus weighted-Jacobi and Gauss-Seidel smoothers]](gs_lex-w_jacvswkb.png)
