The counter-Earth Antigeos system, appearing in the trilogy of novels The Other Side of the Sun (1950), The Other Half of the Planet (1952) and Down to Earth (1954) is described by author Paul Capon in some detail, and it interesting to consider just how plausible this arrangement might be.

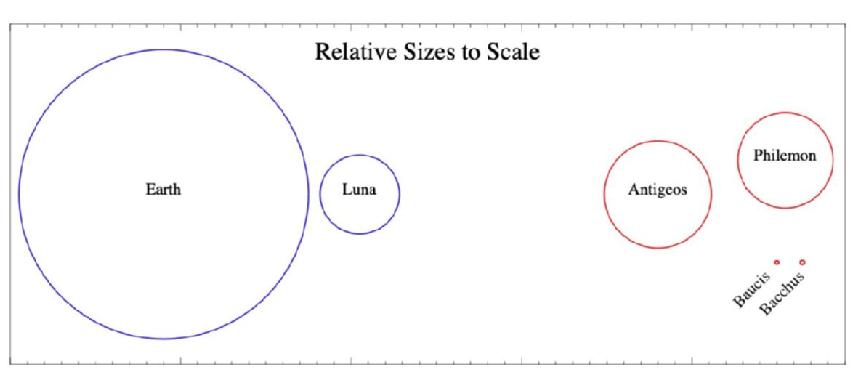
In The Other Side of the Sun Antigeos is described as a little smaller than Earth and orbiting perpendicular to its spin axis, but with two moons which are each the equal to our own Luna in its sky. One is a similar distance to our Moon from the planet, and itself has a moonlet. The other is a little smaller but closer, which suggests a picture like the following:

Over the course of the first novel we learn that

• Antigeos has a 30 hour day and 292.2 days/year
• Philemon & Baucis are 300,000 miles distant,
• Philemon is a little larger in the sky than Earth’s moon, and orbits Antigeos seven times a year
• Baucis is 100 miles diameter, with a 38 hour orbit, and orbits 20,000 miles from Philemon
• Bacchus, Antigeos’ second moon, is closer and smaller, but has the same angular size as Philemon in the sky, and orbits twice in an Antigean day.
• The angle of obliquity to the ecliptic is almost a right angle, i.e. its moons orbit in plane of equator of Antigeos.

As the characters note, calculating the eclipses in such a system must be rather a headache, and the tides likewise.

So, here we have enough information to start calculating some properties of the system and filling in the gaps. I’ve summarised this in the table below. Boxes in green are properties of Earth, the Sun, the counterEarth (Antigeos) and the Moon (Luna) that we know. Yellow boxes indicate the information we’ve been given (where I’ve transformed miles to kilometres and Antigean days to Earth days where appropriate). The notation 1.99E30 indicates 1.99 x 1,000,000,000,000,000,000,000,000,000,000 (i.e. 30 zeroes).

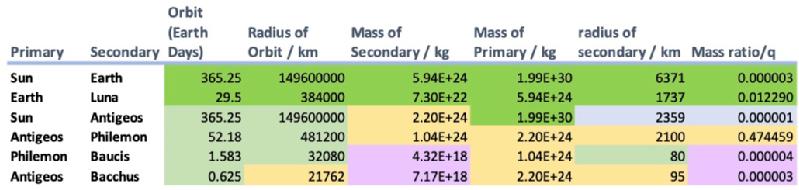
Table: properties of the Antigeos-Earth-Sun systems. Known facts are shown in bright green. Pale green values are given in the text and are treated as assumed facts. Remaining entries are calculated below: Yellow numbers can be calculated from gravitational forces or angular size with no further assumptions. The blue values for Antigeos require the assumption of an Earth-like surface gravity. The purple values for Baucis and Bacchus assume a density of 2000 kg/m³ for these bodies.

The next easiest number to calculate is the mass of Philemon since we’ve been told the period and radius of its much smaller moonlet Baucis. We can just balance centripetal and gravitational forces here:

F = G M m / R² = m R omega² = m R (2 pi/P)²

So M = 4. pi² R³ / P²

where R is the orbital separation, P is the orbital period (i.e. "year"), and M and m are the mass of the larger and smaller body respectively.

This suggests that Philemon has a mass of 1.0E24 kg. This is about a sixth of the mass of Earth, or almost 14 times the mass of the our Moon, Luna - in other words, Philemon is a very substantial moon by Solar System standards. Since we’re told that Philemon is about the same size as Earth’s Moon in Antigeos’ sky, and we know its distance, we can also estimate its radius as about 2100 km, a little larger than Luna.

Since Antigeos is an Earthlike planet, that suggests that it can’t be much more massive than Philemon and this is more likely a binary planet rather than a true planet-moon system, since its centre of mass will lie between the two worlds. Nonetheless we know the typical distance of Philemon from Antigeos and the period of its orbit, so we can repeat the calculation above with minor changes. This gives a total mass for the system of 3.2E24 kg (about half that of Earth), and a mass for Antigeos itself of 2.2E24 kg (only twice that of its own major moon!).

Given a mass for Antigeos, and the orbital period of its minor moon, Bacchus, we can also use the same equations to estimate the distance between them as a little less than 22,000 km, or just a twentieth of the distance between Antigeos and Philemon. Since we’re told that Bacchus and Philemon have the same angular size in Antigeos’ sky, this tells us that it must also be twenty times smaller than its sibling - with a radius of just 95 kilometres.

Now though we have to start making some assumptions. Antigeos appears to have much the same gravity as Earth - the travellers have no trouble moving around, although a character is told that “you’re a trifle heavier on Antigeos than you were on earth…. The planet’s size is less but its density is greater.” (The Other Side of the Sun, Heinemann edition, 1950, pg 195)

Assuming the “trifle” here is only a small percentage, then Antigeos must have the same ratio of mass to radius as Earth, giving it a radius of 2360 km, only a third of the size of Earth - this is a more compact world, and a much denser one than our planet.

Finally, to estimate the mass of the smaller moonlets we must make one further assumption. Both are in a similar mass range to the satellites of Mars or the smaller gas giant moons, all of which are believed to be captured asteroids. So if Baucis and Bacchus have the same composition as the larger asteroids (i.e. density ~2000 kg/m³) we can estimate their mass in the 10¹⁸-10¹⁹ kg range.

So all in all we have a system far more like the following:

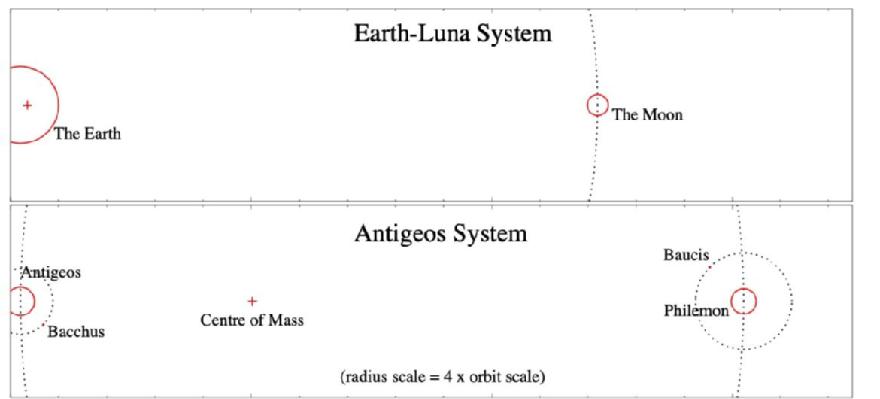
On the lower plot here, I've multiplied the planet sizes by a factor of 4, so the planets can be seen, while the orbits are otherwise to the same scale. The locations of the system centres of mass are indicated with a cross.

One interesting result of the geometry of this system is the effect of tides on Antigeos’s oceans. Tides result from the unequal pull of gravity on two sides of a body due to the increase in distance between them. Here on Earth, the tidal effect we feel from the Sun and the Moon are roughly equal - which is why when the two align we get strong spring tides, while when they pull in conflicting directions we get much weaker neap tides. Antigeos will experience the same solar tides as the Earth. Philemon is comparatively much larger, but also slightly further away from our moon, and the tidal forces scale as M/R^3 so the impact of Philemon will be about a fifth of our lunar tides. On the other hand, while the minor moon Bacchus is much much smaller, it is also much much closer. Counter-intuitively, the tiny Bacchus will produce tides a thousand times stronger than those of our moon, and what’s more, these will sweep around the planet twice a day!

This will cause what is effectively a tidal wave, being dragged around in the planet’s wake. The explorers encounter these waves - first witnessing their effect on a coastal town in The Other Side of the Sun and then experiencing it from the water of Antigeos’s oceans in The Other Half of the Planet. Perhaps unsurprisingly, the local population have a taboo against ocean travel, which probably originated in a prohibition for public safety. In fact, the eye-witness account mentions a tidally-driven pressure wave so severe that breathing is problematic:

"Each time a wave was due I lay flat in the dinghy, strapped myself in, lashed my provisions to the floats, filled my lungs and waited. Amazing experience, of course. At one moment you’re floating on a comparatively calm sea, and at the next you’re riding up a wall of water as if you’d been shot out of a gun. Noisy, too. Naturally. And on the second or third occasion I got caught up in the crest of the wave and found it damned embarassing. Difficulty in getting my breath you know.” (The Other Half of the Planet, Heinemann edition, 1952, pg 183)

Unfortunately, any such pressure phenomenon would be experienced by those on land, as well as those on the water. It’s hard to imagine so severe a feature being confined in its effects, although admittedly Bacchus’s orbit is described as equatorial - passing over Antigeos’ encircling ocean the whole way. While no information suggests it is habitable, it’s also worth noting that Philemon’s own satellite Baucis would also cause strong tides on the larger moon.

On the whole, the system as described appears pretty plausible, with the sole exception that the inferred densities of Antigeos and Philemon are surprisingly high. With a radius a third that of Earth, Antigeos has a volume just 4 hundredths that of our planet, but has a mass that is over a third of ours. As a result, the implied density of Antigeos is almost ten times higher than that of Earth rock (rho_antigeos = 40,000 kg/m³, rho_Earth = 5,480 kg/m³). Philemon must be similarly dense (rho_philemon=26,900 kg/m³). This puts the density of both twin planets in the range of Osmium, the densest material known (short of the degenerate matter found in the heart of stars). On the whole, this seems unlikely. However it’s worth noting that the values Capon estimated for his planetary system were fairly approximate, and that a relatively small difference in the assumed surface gravity or angular size of the planets might bring this number down by a factor of a few, putting it into more comfortable territory. Capon himself was a television editor and children’s writer - not a professional scientist. The fact that his books provide so much detail on the physics is itself interesting, as it suggests that readers at the time were expected to understand such quantitative information, or at least have a feel for its plausibility and the authority it lent to the text.

Given the generally good descriptions of the physics in these novels, there is one glaring error - which should probably be considered a narrative conceit for the sake of the story. Early in the first book, a newspaper report tells us:

Can we rocket into space and visit the hidden planet? Rocket-expert Roland Tugg thinks, Yes. It's much easier, he says, to send a passenger-carrying spaceship to Antigeos than to either Mars or Venus. Quoting him: 'Far fewer difficulties would be encountered in traveling along our own orbit than in travelling from this orbit to that of another planet. In fact, to visit Antigeos it wouldn't matter if you didn't travel at all once your spaceship had escaped from earth's gravitational pull. Sit in space and the earth will recede from you at the speed it goes round the sun - eighteen and a half miles a second, more than a thousand miles a minute - and Antigeos will rush towards you at the same speed. (The Other Side of the Sun, pg 46)

For a supposed rocket expert, the fictional Tugg has a surprisingly poor understanding of orbital physics. Not only is it unclear how the spaceship is meant to shed that eighteen and a half miles of second of orbital speed to "sit in space", but any spaceship attempting that will simply fall inwards towards the Sun, long before Antigeos arrived. Unfortunately, the rest of the characters, and the physical laws of Antigeos's universe seem to agree with Tugg. For the sake of the story, it makes for a convenient explanation for what would otherwise be a complex and energy-hungry orbital manoeuvre.

Despite the error or orbital physics and the rather extreme density requirements of Antigeos, it seems clear that Paul Capon visualised a surprisingly plausible counter-Earth system, and that his books provide an interesting little insight into the possibilities of the now-ruled-out possibility of lands unknown on the other side of the Sun.