Research Interests
| Quantum metrology | Quantum and gravity | Quantum complexity | Quantum verification |
|---|---|---|---|
 |
 |
 |
 |
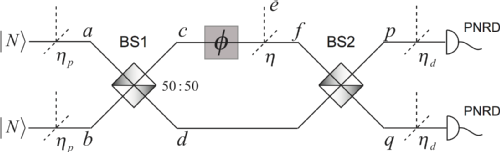
Quantum metrology : Metrology is the science, and art, of estimating a parameter precisely. It is a fundamental aspect of investigative science, as well as technology and commerce. Our interests lie in uncovering the fundamental limits that the laws of quantum mechanics impose on the precision of estimating a single or multiple parameters. In principle, the limits imposed by quantum mechancis allow more precise estimates than those possible using classical resources. These improvements rely on purely quantum phenomonenon such as quantum entanglement and squeezing, and span both discrete variable (spins, qubits) and continuous variable systems.
We invent and analyse new scenarios where quantum resources can be employed to attain quantum-enhanced sensing, imaging, microscopy, and spectroscopy.
Potential students must have strong interests in quantum information theory, probability theory, and quantum optics.
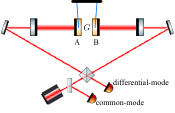
Quantum aspects of gravity : Whether gravity as one of the fundamental forces of Nature must have a quantum description is much-debated. Quantum information science may provide a new perspective on this debate. Much-needed experimental inputs may be provided by recent experimental advances in quantum optomechanics.
We study the effects of gravity in table-top quantum mechanical systems. Our aim is to design and theoretically analyse experiments that may provide evidence for or against the quantum nature of gravity in the laboratory.
Potential students must have strong interests in quantum information theory, quantum optomechanics, general relativity, and quantum field theory.
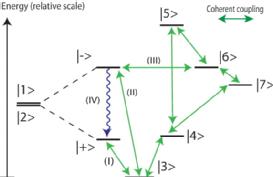
Quantum complexity : Whether quantum mechanics plays a role in life processes in an intriguing question. It surely does, since the stability of matter and the nature of chemical bonds are quantum mechanical. Indeed, any process analysed at a length scale small enough and time scale short enough will exhibit quantum behaviour. The first step in constuting a well-posed question is therefore to identify the phenomenon of interest, and then study the role of quantum mechanics on length and time scales relevant to the phenomenon.
We study complex quantum phenomena such as excitonic energy transport in light-harvesting complexes, or ultrafast isomerisation in rhodopsin which is the primary photochemical event in vision. The complexity arises due to the blurred boundary between the system of interest, and the surrounding environment. Identifying and quantifying this quantum complexity is one of our interests. We also seek to understand the role of quantum correlations in these phenomena. To that end, to study novel spectroscopic techniques - possibly augmented by quantum optical probes.
Potential students must have strong interests in quantum optics, quantum nonlinear optics, quantum light-matter interactions, and quantum information theory.
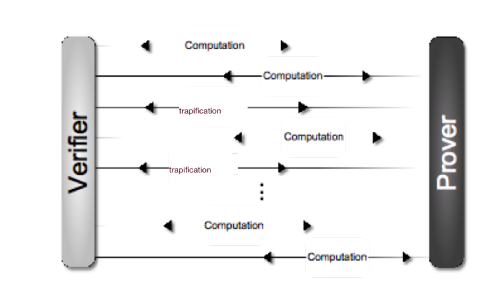
Quantum verification : If a quantum computer factorises a number so large that it has never been factorised before, the correctness of the answer can be checked efficiently on a classical computer. However, if a quantum simulator performs a simulation so hard that it had never been simulated before, how do we assure ourselves of its correctness? This is even more vital if the quantum simulator is noisy.
We devise means of determining the correctness of noisy quantum computations. One of our recent methods is quantum accreditation - a practical and scalable method of placing an experimentally measured upper bound on the correctness of any noisy quantum computation. This is based on ideas from interactive proof systems in theoretical computer science. The validity of accreditation, and any similar tool relies on the validity of the assumptions made in a given quantum hardware. We are thus led to studying means of testing these validities as well.
Potential students must have strong interests in quantum information theory, quantum computation and error correction, and quantum simulations.
Past interests
Quantum correlations : Identifying the resources that make quantum enhancements possible is an abiding question in quantum information science. Although quantum entanglement is generally believed and frequently claimed to be the main resource, it is not so in all cases. A rigorous proof only exists for the necessity of multipartite entanglement for exponential speedup in pure state quantum computation. What about mixed state quantum computation ? Or non-universal models such as the one pure qubit model, boson sampling, instantaneous quantum computing, and quantum simulation in general. And what about other information processing tasks like communication, cryptography, or sensing ?
We study measures of quantum correlations more general than quantum entanglement. The foremost is quantum discord, but by no means the sole one. We also study how such correlations can be generated and detected in principle, as well as in practice in physical systems. Another aspect is the opertational interpretation of these new measures in terms of quantum information processing tasks. We use the resource theory of quantum information and the family of quantum protocols such as the fully-quantum Slepian Wolf protocol. While these questions are typically studied in the context of finite dimensional systems, we are interested in continuous variable version was well, where non-Gaussianity plays a central role. This takes us deep into the heart of quantum information processing, opening up new ways of attaining quantum enhancements in information processing.
