The purpose of a computer program is to describe methods of solving certain problems. It is necessary to represent a problem somehow in the program. Many (if not most) programming languages have variables and procedures. The variables refer to some storage spaces to hold data representing objects (e.g. the coordinates of an object). A procedure is a sequence of instructions telling the computer how to calculate the data stored in the variables. Due to the side effects of some instructions, the data can be converted into human readable forms, e.g. the write statement in Fortran can display data in a specified format.

An interior designer might like to draw a picture of a room with some furniture inside it on the display screen. Suppose there is a program which allows a user to enter the coordinates of these objects through the keyboard. This program can redraw the objects if the user issues a ``refresh'' instruction, or more conveniently, redraw the objects automatically after new coordinates have been entered or existing coordinates changed. It is not difficult to write this kind of program in conventional procedural languages, such as Pascal or C. Some existing software, like MacDraw or some CAD packages, let the user manipulate graphical objects. These packages do the job quite well since they have highly interactive user-interfaces.

However the interior designer may require more than just refreshing the display of the objects on the screen; he may wish to specify some of their relative positions. For example, he may also like to put a lamp at the centre of the table no matter where it will be. That means the coordinates of the lamp are determined by the coordinates of the table. In this case, he has to calculate the new position of the lamp and redraw it after it has been moved. Since he may move the table several times to see which position is better, he will be required to repeat the same process ? calculate new coordinates and redraw the objects. Obviously it is a tiresome and error-prone job especially when the number of objects and definitions becomes large.

Some software packages, such as MacDraw, allow the user to group several objects into a single large object. The user can then manipulate the object using the operations provided by the packages. The grouping of objects preserves the relative coordinates and attributes of the objects among the same group during the manipulations. Hence, if a table and a lamp are grouped together, translation of the table will also translate the lamp by the same amount. However grouping objects also puts extra restrictions on the objects. For instance, the enlargement of the table will also resize the lamp in the same ratio, and this may not be the intention of the user. The method of grouping objects provides very restricted transformations on objects. Complicated definitions of objects, such as

``C lies at the mid-point of line AB, where endpoints A and B are defined independently'' -- (1-1)

cannot be specified by this method. Thus the method of grouping objects can only be considered as a macro manipulation on a number of objects.

Therefore it is much more convenient to allow the user to specify the abstract definitions of the objects in terms of other objects. For example, the point C described in (1-1) can be defined in terms of points A and B mathematically as below.

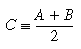
A system that can manage definitions is called a definitive system or definition-based system.

The use of a definitive system to describe geometric relationships also has another advantage. Many CAD systems allow the user to specify parametric objects, i.e. generic objects whose size and position can be determined by giving parameters. In conventional systems, such objects are represented by small procedures comprising appropriate sequences of drawing instructions, but a method of specifying the relationships between parts of the object explicitly is preferable. For example, contrast the two specifications of a square with given corner and size below.

(1) Procedural

(2) Definitive

In the first example, the size and position of the corner are fixed when the symbol is drawn. In the second example, the object specified by the definition:

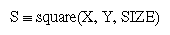
would be re-defined if the value of the variable SIZE were to change.

Unfortunately, conventional languages do not provide any built-in facility to help writing a definitive system. Thus the programmer must write a detailed definition manager to handle the definitions.

A well-known example of a system based on definitive principles is the spreadsheet software which has recently become so popular in business and personal accounting applications. A spreadsheet is a program that provides us with a large grid of cells into which we can put in numbers and formulae. A cell that contains a formula causes the system to re-calculate the formula whenever any cell on which it depends is changed, and display the new value on the screen automatically. The display action is implicitly invoked by the system after the re-calculation. These actions can be called implicit actions because they are pre-defined in the system.

The make command in UNIX^TM is a good example of file maintenance software. Unlike the spreadsheet software, the user has to specify the updating action in a file (the makefile) explicitly. These actions can be called explicit actions. For example, to express the fact that ``object file.o is compiled from source file.c'', the appropriate makefile is:

file.o : file.c
        cc -c file.c

The first line indicates the dependence and the second line contains a UNIX command showing how the object file can be compiled from the source file. The explicit actions allow less restricted updating actions to be defined. For example, the user can give different options to the compiler or use different compilers to compile the target object. However the user has to make sure that there are no destructive side-effects.

In a definitive system, each definition has one and only one target object (such as a cell or an object file). Usually there is at least one source objects. The target object is said to ``depend on'' the source objects because it is computed from them only and whenever the values of the source objects change the target object must be re-computed. No cyclic definitions are allowed since recursively defined definitions lead to meaningless definitions, such as ``''.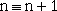

A spreadsheet program and the make command are driven by definitions. Although make is more like a dependency maintainer (it keeps track of objects by referencing the dependence, but does not refresh the target object), it combines representation of data dependencies with explicit actions resembling those needed to maintain definitions. Actually a definitive system can be implemented using a dependency maintainer with some built-in computing utilities. Internally, a system builds a dependency graph according to the definitions given and uses this information to determine which data has to be updated; from the formula of the definitions, it knows how to compute the targets.

A definitive system saves us from remembering what has to be updated when certain data have been changed. It is especially useful in a continuously changing environment; for instance, a programmer would use make to compile those modified modules of a large project under development. The success of spreadsheet programs and make has illustrated the advantages of a definitive paradigm.

Another advantage of a definitive system is regarding human-computer interaction. Some definitive systems can be programmed to echo the up-to-date data on the display as soon as certain data has been changed by the user. The user can know the result of the change immediately and then continue to modify the definitions. This interactive behaviour of the definitive system may contribute to applications, such as computer aided design (CAD) systems, that require intensive human interaction.

Definitions are also good for specifying relationships between objects. The side-effects of updating actions are able to simulate the actions of objects responding to a change in the environment.

An implementation of a definitive system is not a trivial task. As mentioned earlier, it may involve developing a complicated dependency maintainer. It is more sensible to make a general purpose definitive system and build a special purpose system front-end on top of it. Unfortunately no such systems are publicly available. An experimental language EDEN - an evaluator of definitive notations (see Edward Yung's MSc thesis) - was designed to try to fulfil this purpose. It was designed to be a general purpose language supporting definitions. Users can define their own procedures and functions using some C-like statements. An interpreter can be customized for different applications. The first prototype of such an interpreter was implemented in 1987. Since that time, another prototype of the same language has been implemented. The difference between these two versions is mainly concerned with the internal evaluation strategy, and is transparent not noticed by the user, and should not concern the naive user.

Eden is a hybrid language that combines elements of traditional procedural and definitive languages. (note: some people use the term definition-based languages). It has both advantages and disadvantages of procedural and definitive languages. This user handbook is a guide to the Eden programming language.