Making construals as a new digital skill
Dissolving the program - and the programmer - interface
Meurig Beynon, Jonathan Foss, Elizabeth Hudnott, Steve Russ, Chris Hall, Russell Boyatt, Emma King
University of Warwick UK
wmb@dcs.warwick.ac.uk
Hamish Macleod, Jen Ross
University of Edinburgh UK
h.a.macleod@ed.ac.uk
Dimitris Alimisis, Emmanouil Zoulias, Rene Alimisi
Edumotiva Greece
info@edumotiva.eu
Erkki Sutinen, Ilkka Jormanainen, Carolina Islas, Andrés Moreno
University of Eastern Finland Finland
ilkka.jormanainen@cs.uef.fi
Piet Kommers
Helix-5 The Netherlands
pkommers@gmail.com
Peter Tomcsanyi, Michal Winczer
Comenius University Slovakia
tomcsanyi@slovanet.sk
© © 20xx IEEE. Personal use of this material is permitted. Permission from IEEE must be obtained for all other uses, in any current or future media, including reprinting/republishing this material for advertising or promotional purposes, creating new collective works, for resale or redistribution to servers or lists, or reuse of any copyrighted component of this work in other works.
Abstract Making a construal is a way of using the computer to help us in making sense of a situation. Its merits as a new digital skill for developing open educational resources in the constructionist tradition are illustrated using a basic construal of shopping activity. Making construals is the central theme of the three year EU Erasmus+ CONSTRUIT! project. This paper takes the form of an introductory tutorial highlighting key qualities of construals that will shape the CONSTRUIT! agenda.
Keywords construal; computing; spreadsheets; educational technology; school education; constructionism; open educational resources; educational games; software development
I. INTRODUCTION
A construal is an interactive artefact that we develop to help us explore and record our emerging understanding. The term 'construal' was introduced by David Gooding [1] to refer to the techniques that Faraday used to make sense of electromagnetic phenomena in the 19th century. Making construals by computer has been a central theme of a research project undertaken by staff and students in Computer Science at the University of Warwick over the last thirty years (cf. [2], [3]). Educational applications [4], puzzles [5], [6] and games [7], [8] have been topical in this research. Wider dissemination and further development of the principles and environments for making construals is currently the subject of a three year EU Erasmus+ project, led by Warwick, with five partners drawn from Greece, Finland, Slovakia, the Netherlands, and the UK [9].
Making a construal differs from writing a program. Rather than specifying a recipe to achieve certain functional goals, it establishes an open-ended context for interaction within which the human and automated agency in a domain can be expressed. Within this environment, program-like behaviours can be crafted by the maker and enacted by the computer. This allows the traditional roles of the human agents, whether users, learners, players, designers, teachers or developers to be integrated and unified. This has significant potential implications for education and for computer games. For instance:
- the premise of constructionism [10] is that learners can develop learning resources and thereby to some degree assume the roles of teachers and developers;
- license to change open educational resources [11] is only useful in so far as teachers and learners are technically able to modify software to meet new requirements;
- the computer games community embraces 'mods' that enable players to change the rules [12], thereby blurring the distinction between user/player and developer roles.
This paper illustrates these distinctive characteristics of making construals with reference to simple examples that have been developed with schools education in mind. Its three main sections take the form of an introductory tutorial on making construals online in JS-EDEN [13]. This is a prototype special-purpose environment for making construals (“the MCE”) that is to be developed throughout the CONSTRUIT! project. A companion paper is in preparation [14]. This will reflect on the concept of ‘making construals as a new digital skill’ from several different perspectives and so help to inform the future agenda for the project.
II. BASIC PRINCIPLES OF MAKING CONSTRUALS
Some orientation is needed to understand the notion of ‘making construals’ as a new digital skill.
A. Construals and Programs
The key difference between a construal and program relates to the way in which it acquires its meaning. A program can be regarded as a formal recipe for action that has an abstract functional specification (expressed in logical terms), a concrete implementation (expressed in code) and a user-interface (comprising widgets for visualisation and manipulation that enable the user to execute the specified functions). By contrast, a construal is interpreted within a quite different semantic frame.
A construal is conceived not as a program with an abstract functionality but as an artefact that exploits the computer and associated technologies to offer an interactive experience to its maker. The term ‘artefact’ is chosen to emphasise that what is important about a construal is embodied in its physical realisation. The term ‘maker’ is adopted to signal that (as in the appreciation of a work of art, for instance) a construal is not associated with a specific functional objective.
In some sense, the most essential elements of a construal are quite the reverse of what is typically regarded as the essence of a program. That is to say, computer science places its primary emphasis on the program as the concrete embodiment of an abstract algorithm with a specific function. The way in which this functionality is presented to the user through concrete features of the implementation is of course of great interest. But, from a theoretical computer science perspective, how the interaction with a program is experienced by the user is a peripheral issue.
B. The Semantics of Construals
For a theoretical computer scientist, the most disconcerting aspect of the notion of ‘making construals’ is that – like the appreciation of works of art – it is an activity that has no formal semantics. This is potentially a reason for questioning its suitability as an application of computing. To understand how this objection is to be countered, it is helpful to consider the way in which meanings are already being associated with computer artefacts to great effect.
Consider what is involved in the interpretation of a spreadsheet in a familiar application such as recording and evaluating examination marks. There is a correspondence between (respectively) the rows and columns of the spreadsheet and the students and their examination subjects. Anyone who has experience of studying examination grids will be aware that the connection between ‘looking at a row / column’ and ‘thinking about a student / examination’ is quickly taken for granted. To the examiner ‘the row’ and ‘the student’ are registered as one entity, even though it is perfectly possible to attend to ‘a row of numbers’ and ‘the set of examination marks obtained by Josephine’ as separate experiences. Likewise, one can attend to a single entry in a row and make the same direct association with ‘Josephine’s mark in Empirical Modelling’.
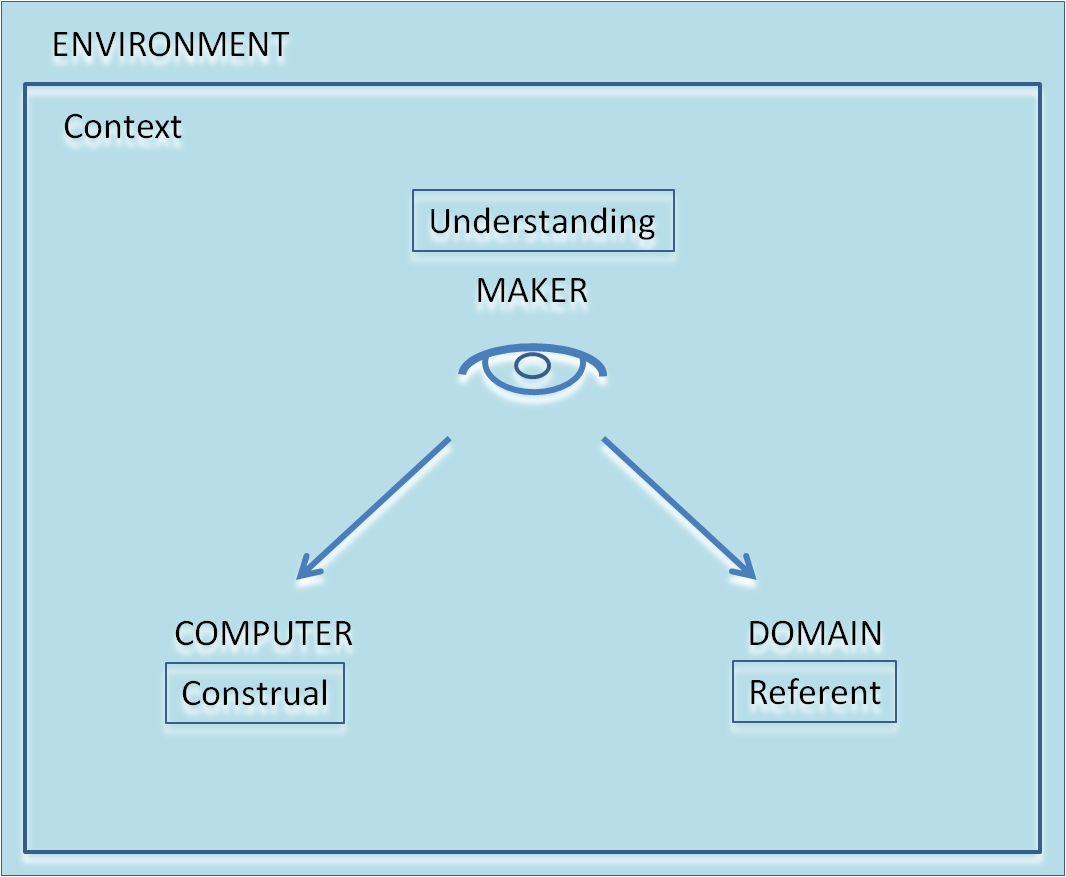
Figure 1: Making a Digital Construal
In this context, what connects the spreadsheet with its meaning in the examiner’s experience has to do, not just with its abstract formal content (“the raw examination data”), but with its concrete representation. The data is realised and disposed in a way that exploits features of our human perception so that a connection can be experienced. The informal semantics that underlies ‘making construals’ is based on an empirical premise: that computer-supported realisation and disposition of abstract values and structures has the power to invoke meaningful connections for the maker.
Of crucial importance is the role of interaction with the construal. The examiner’s confidence in the interpretation of the spreadsheet is in fact based on a foundation of faith in the integrity of the processes that have gone into its specification and construction. It is curious that the ‘final’ examination grid is conventionally reviewed as a static artefact when in fact its significance rests on myriad potential interactions that might subvert the entire examination process. It would be most alarming if Josephine’s overall average mark decreased when we awarded an extra mark to her Graphics paper. To appreciate the richness and subtlety of the semantic model that underlies the spreadsheet, it is helpful to reflect on the personal private nature of the connections between marks and students in the minds of different examiners and to consider what implicit assumptions are being made about the way in which the values and relationships in the examination grid have been entered and specified.
Figure 1 is a diagram to describe the key ingredients that inform the state of mind of the maker of a construal. Building a spreadsheet from scratch, using it and subsequently refining it is the kind of activity to which Figure 1 refers. The diagram is to be interpreted as a snapshot of the moment-by-moment experience of the maker. The construal, the referent, the maker’s understanding and the context are at all times fluid and changing.
In the examination scenario discussed above, the construal is the spreadsheet, the person who is interacting with it is the maker, and its referent is the cohort of examinees to which the spreadsheet refers. The connection that is suggested by the two arrows that emerge from the eye icon is a connection in experience of the kind that was alluded to above. (The maker is so-called as the person who makes this connection.) The context is the setting for the interaction: a typical exam board meeting, in which the maker has some familiarity with the cohort of students being examined and the examination structure associated with their course. The maker’s understanding is associated with all the putative interactions with the spreadsheet that would conform to their expectations. For instance, the examiner ‘knows’ what would happen if they were to increase Josephine’s mark in Graphics, at any rate in the empirical sense that if necessary they could confirm this to be ‘as expected’.
When the maker is building the examinations spreadsheet from scratch, another context is significant. In the initial stages of the construction, there might be no specific cohort of students in mind. The maker’s focus is on establishing a connection in experience between the construal that is under construction and a referent that is simultaneously taking shape in their imagination. In this process of construction, such connections do not have the robustness and objectivity that pertain at a final year exam board. The maker crafts the construal through experimental interaction and reflection, seeking to set up a connection in experience that enriches their understanding and may eventually be shared. The association of meaning with the construal necessarily has an empirical pragmatic quality – it does not have the sharp, exact, ideal but brittle character of a formal meaning. Repeated interaction with the construal and its referent that reinforces the experience of connection, perhaps even to the extent that it is taken for granted, can give greater confidence in the quality of the construal. As is appropriate in the learning process, the possibility that our construal does not adequately account for what we learn about its intended referent remains. On the other hand, flaws in a construal do not necessarily or typically have the same undermining impact as logical flaws in a formal development. For instance, we might not know that there is some minor error in a formula even in the final examination grid. But in good exam board practice, where critical data values are given extra scrutiny, it is unlikely that such an error would be overlooked and still have a significant impact on the degree outcomes.
The informal semantic model proposed here may seem to lack substance when set beside the logical foundations for the theory of algorithms that are supplied by the work of Boole, Frege and Turing. The notion that the connections we make between experiences are themselves given-in-experience is not a new idea however – it is the cornerstone of William James’s philosophical stance, as elaborated at length in his Essays in Radical Empiricism [15]. For the reader’s peace of mind, the most important message in James’s account is that the connections we make in experience are empirical in nature, and it is appropriate to accept them without seeking a reductionist explanation. Where grasping the nature of these connections is concerned it is helpful to think of the way in which familiar words evoke meanings, so that the process of constructing a text is inseparable from its intended meaning.
The role that learning plays in this context is appreciated when we consider whether we could read and write with the same fluency in Greek, Thai or Finnish. And if we are to make appropriate construals of our language understanding, then without doubt they will have to be expressed in terms that go far beyond a binary ‘correct’ and ‘incorrect’.
C. The Constitution of Construals
The practice of creating interactive artefacts to express our understanding of a situation or phenomenon is of course well-established. It is natural to ask whether any interactive artefact can fulfil the role of the construal in Figure 1. In fact, the choice of the examinations spreadsheet as an illustrative example of a construal is significant. As is well-recognised, spreadsheet models have distinctive qualities where ‘what if?’ questions are concerned. In this respect, the process of making a connection in experience between interaction with the construal and with the referent relies crucially on the way in which the construal has been composed – its constitution.
Three key constituents of the spreadsheet establish its status as a construal: observables (entities to which we can attribute an identity and a current value), the dependency amongst observables (how a change to the value of one observable in one and the same action entails a change to the value of another) and the agency that acts upon them (as represented by human or machine actions that are deemed to be responsible for changing the values of observables). The connection between the construal and its referent (to be engineered by the maker) relies on constructing counterparts within the construal for each of these features of the referent.
By way of illustration, observables in the examination spreadsheet include the student identities, their marks in individual subjects and across the entire curriculum, the average mark for each examination and for each student. The average mark for an examination is defined by a dependency that is expressed by an associated formula. Examples of agency include the entry of exam marks into the grid by the examination secretary, or the correction of an exam mark by the examiner. The counterparts in the spreadsheet of these observables and dependencies are the cells, rows and columns of the grid, which are disposed in such a way that the connection can be readily established, and can acquire the subliminal quality that attests to being given-in-experience.
The examination spreadsheet illustrates the role played by observables, dependencies and agency in making construals. To derive an environment resembling JS-EDEN from a spreadsheet involves exploiting its more advanced features, such as placing user-interface controls on sheets and introducing alternative modes of visualisation. It so happens that the rows and columns of a grid are well-suited for visualising students and subject marks, but in other contexts much richer varieties of visualisation and manipulation are required. The maker’s perspective on the construal in the semantic framework depicted in Figure 1 also encompasses more than is expressed by ‘the current state of the spreadsheet’. The observables associated with the construal in Figure 1 must trace each change in the way that the state of the construal is experienced by the maker. That is to say, the construal associated with a spreadsheet would in general include explicit observables to record such issues as ‘which spreadsheet cell is the current focus of the maker’s attention’.
III. AN ILLUSTRATIVE EXAMPLE OF A CONSTRUAL
The characteristics of the prototype MCE and the qualities of construals will be illustrated using a simple example.
The topic for our illustrative construal will be ‘shopping’. This potentially has educational interest in many different ways. We might wish to introduce students to managing coins and purchases in a ‘life-skills’ lesson. The emphasis might be on the coin recognition or on the mental arithmetic this entails. The educational resources to be developed might take the form of interactive environments that can scaffold learning about currency and shopping protocols. They might be educational games (cf. [16], [17]). More advanced topics, such as algorithms for giving change, and how these are influenced by the denominations of coins available, might also be addressed (cf. Greedy Algorithms and the Making Change problem [18]).
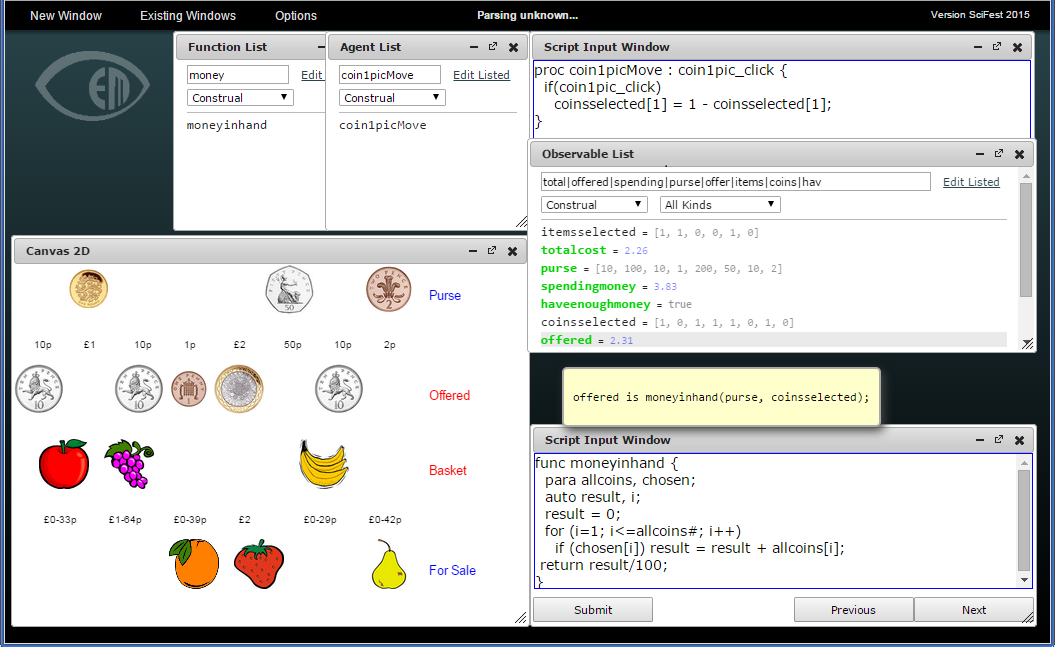
Figure 2: A basic Shopping construal
A basic shopping construal is depicted in Figure 2. It relates to a situation in which the maker is acting in the role of a customer in a shop selling fruit. For simplicity, the fruit for sale comprises six items. An item that is selected for purchase is displayed in the basket – the customer can place each item in and out of the basket by clicking on it. The coins that the customer has available for payment are initially displayed in the purse. Clicking on a coin in the purse simulates offering it in payment – clicking a second time will restore the coin to the purse.
In this shopping scenario, the items for sale, the items selected for purchase, the coins being offered and the coins that remain in the purse are simple examples of observables. Other observables include the set of items in the basket and the prices of the individual items. These observables are visually represented in the Canvas window. There will be other ‘observables’ in the customer’s mind, though these are not directly visible. The customer will need to know the total cost of the items in the basket, and how much money has been offered. The values of these observables are determined from the prices of the items selected, and the selection of coins that has been offered, and they are both defined by dependency. These ‘real-world’ observables also have counterparts that have not been visualised in the construal.
As the display in Figure 2 shows, there are many ways in which to explore a construal within the MCE. In addition to the Canvas window, there are instances of Observable and Function lists. The amount that has been offered in payment is recorded in an observable called ‘offered’ which – being determined by a dependency – is highlighted in green in the Observable List. Its current definition appears in a box below:
offered is moneyinhand(purse, coinsselected);
In this definition, ‘coinsselected’ is a list of booleans to specify which of the coins in the purse have been offered in payment. Interaction with the construal readily demonstrates the significance of this observable: clicking on a coin will negate the value of the associated boolean in the list.
Observables with values implicitly defined by formula or explicitly specified are the core constituents of the construal. They are recorded in a comprehensive ‘script’ of definitions, from which definitions can be selectively displayed in an Observable List. The other generic features of the MCE, the Functions and Agents are also illustrated in Figure 2. The function ‘moneyinhand’ is used to express how the amount offered is determined by the content of the purse and the coins selected. This function is defined with a simple fragment of conventional procedural code, written in the EDEN language[19], as shown at the bottom right of Figure 2.
The agency of the customer is reflected in the actions that select items and coins. The action that is associated with clicking on the first coin is shown at the top right of Figure 2. This toggles the first boolean value in the ‘coinsselected’ list. The location of the coin icons is determined by a dependency on the value of the ‘coinsselected’ observable. This reflects the fact that ‘offering the first coin in payment’ is in some sense one and the same thing as ‘taking it out of the purse’.
The Shopping construal also illustrates the notions of understanding and context as referenced in Figure 1. It is quite apparent that our familiarity with currency develops through practice to the point where offering appropriate coins for a purchase no longer requires conscious thought. We are also able to recognise when someone is unfamiliar with a currency even when they always offer enough money. The strategies that are followed by purchasers are highly personal in nature. For instance, they may be motivated by extraneous factors, such as the rarity value of the coins themselves. Where context is concerned, one of the most obvious elements missing from the basic Shopping construal is the distinction between ‘window shopping’ (“thinking about what we could in principle buy”) and making a purchase. There comes a point in a transaction when the selection of items is fixed, the money has been spent, the change can no longer be renegotiated and the fruit can be eaten. The role of context in Figure 1 is to reflect the way in which such shifts of perspective transform the perception of state, making it possible to entertain observables of an entirely different nature, such as ‘a poor deal’, ‘a bargain’, ‘undercharged’. It also accommodates scenarios such as cashing in unwanted gifts.
The basic shopping construal can be accessed online (cf. [13]) by following the guidance in section A of the online tutorial resources. The discussion of the construal throughout this paper is most easily understood if read in conjunction with live interaction with the construal. For this purpose, you can exploit the features of the MCE that are illustrated in Figure 2. The Observable List and other resources cited can be accessed via the New Window menu.
A. ‘Making Construals’ and Constructionist Learning
In making a construal, the core activity is the incremental creation of the script of observable definitions. For this purpose, the maker typically enters definitions directly into an Input Window within the MCE (cf. Figure 2). The script is built up in conjunction with exploratory experimental interaction directed at crafting the connection in experience that is depicted in Figure 1. The process of nurturing this connection is ongoing: it has the effect of both reinforcing and testing the construal. In the basic Shopping construal, there is an error in the definition of ‘haveenoughmoney’ – the observable that records whether or not the amount of money the customer has in total (‘spendingmoney’) is sufficient:
haveenoughmoney is totalcost < spendingmoney;
This error can be corrected by specifying ‘less than or equal’ in place of ‘less than’ in the defining formula above and submitting the revised definition via an Input Window.
Changes to a construal can also be effected by agents acting in other roles. If the construal in Figure 2 is being used in the classroom, the teacher might wish to modify the scenario by changing the prices of the items or the coins in the customer’s purse. For this purpose, relevant observables to redefine are ‘price2’ (the price of the second item) and ‘ix3’ (the index that determines the denomination of the third coin). The Input Window is the default interface for making such revisions, but it is not the most appropriate for all agent roles.
In the Shopping construal, the customer – or the learner – would not normally be expected to make use of the Input Window: they interact by clicking on the coins or items. Note that the effect of clicking on the first coin is to invoke a computer-animated agent to redefine the value of an observable. Variants of the construal also include agents that are not accessible via the Canvas interface but can be directly invoked in the Input Window, such as might initialise the purse to a set of randomly chosen coins. As a general principle of making construals, all changes of state – however enacted – have the effect of redefining observables. To be more precise, each agent action redefines the value of a single observable, and it may be that two or more agent actions are performed simultaneously.
The way in which this mode of state changing applies uniformly to all agency is the key to blurring the roles of different agents, as is appropriate in a constructionist learning setting. It may be appropriate to restrict the learner’s access to the construal to what can be modified through interaction via the Canvas window. The semantic distinction between one definition and another is otherwise an informal one: it is in principle possible for a human agent with access to the Input Window to enter any redefinition whatsoever, but whether they can conceive and make sense of their action depends crucially on their expertise and prior experience. The nuanced differences between possible roles are reflected in Figure 2 by the nature of the context and the maker’s understanding.
The conceptual simplicity of the state-changing model for a construal contrasts with traditional programming languages – even those, such as Scratch or Logo, that are intended to promote the idea of learning through constructing. Whereas the interfaces through which developers, teachers and learners act are conventionally sharply differentiated, redefining observables via the Input Window is in principle an activity that is accessible to all. For instance, it requires relatively little specialist skill for a learner to identify that the original definition of ‘haveenoughmoney’ in the Shopping construal is flawed, and making the correction is conceptually simple. It is in this sense that making construals can be seen as dissolving the program interface.
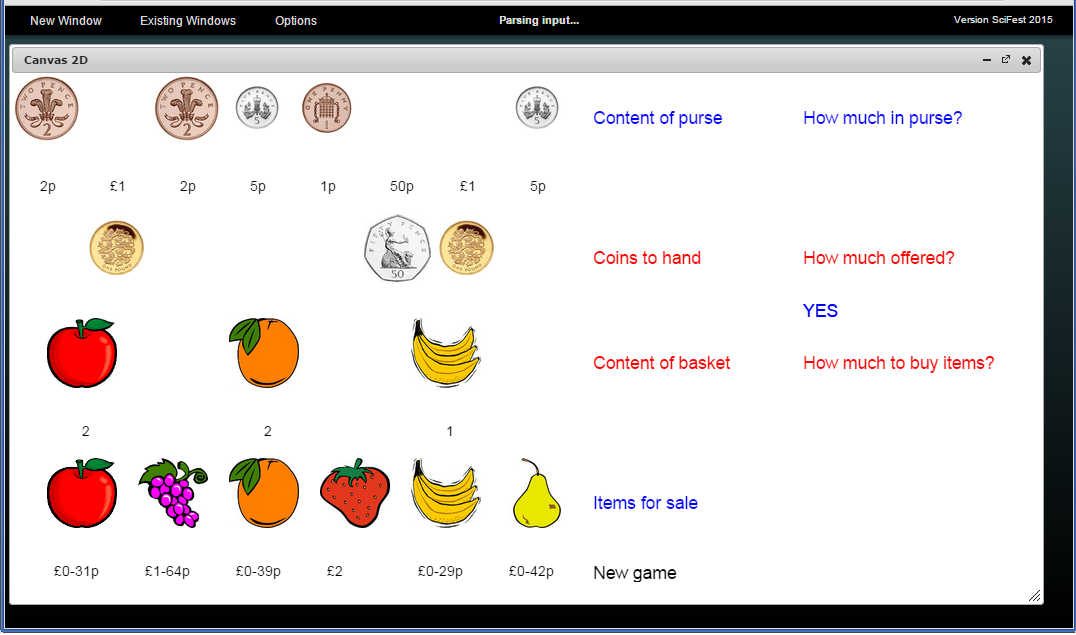
Figure 3: A Shopping-with-stock variant of the Shopping construal, as extended to scaffold learning
B. Deriving Open Educational Resources from Construals
Legal entitlement to make revisions of open educational resources (OERs) is a privilege that is valued by teachers. Its practical usefulness is limited unless OERs can in fact be effectively revised without a developer’s knowledge and skills. Making construals addresses this issue by giving the educationalist a much more accessible point of entry to the developer's world. This may not allow the teacher to play the developer's role but transforms the dialogue between them as design participants to a more coherent and simpler form – thus dissolving the programmer interface.
This can be illustrated with reference to the extension of the Shopping construal depicted in Figure 3. In this variant of the shopping construal, a customer can buy several instances of each item, and the number of items of each kind that has been selected is recorded below the image of that item in the basket. The interface is also adapted so that clicking on an item for sale adds one more instance of that item to the basket, and clicking on an item in the basket removes an instance of the item from the basket.
If the basic Shopping construal had been implemented in a conventional way, a teacher who wished to make this extension would need specialist programming knowledge. There is in general no clear strategy by which it is possible to transform one program to another even though they appear to have many common features. In extending the basic Shopping construal, there is an approach for which the specialist skill required is limited to being able to identify the existing observables whose definitions need to be revised or replicated, and editing their defining formulae. This can be illustrated by considering how the display of items in Figure 2 must be revised.
In the basic shopping construal, a single image is used to designate each item, and whether or not this item has been selected by the customer is indicated by its location on the display. In the Shopping-with-stock construal, there must be an image to denote instances of each item that has been selected by the customer, an image to denote instances of the item that are still for sale, and a means to display the number of instances of each item being bought. Informally, it is clear that in order to transform the basic Shopping construal into the Shopping-with-stock construal, it is necessary to have two copies of the item icons, one of which designates the items to be purchased and the other the remaining stock. The agency in the basic Shopping construal must also be adapted. For instance, in the shopping-with-stock extension depicted in Figure 3, the actions associated with clicking on the items have been revised so that they no longer move items but instead increment counters to record how many instances of each item have been put in the basket.
Having conceived such relationships between observables in the two construals, the next task is to find out the names of the relevant observables. Since the naming conventions can be quite arbitrary, there is no formal procedure to follow, but there are many useful heuristics. The observables associated with the elements that are displayed can be found by inspecting the definition of the ‘picture’ observable for instance. (There is always a ‘picture’ observable associated with the canvas, and its value is a list of the ‘drawable’ objects on the display.) The names of the elements on the screen can then be identified by redefining ‘picture’ in an exploratory fashion. Once a single observable name has been found, others can be derived by using a Dependency Map viewer to find observables that are directly linked to it via a dependency relation, and consulting an Observable List to find its definition and (if applicable) the names of the functions and the observables upon which it depends. It may also be helpful to enter search expressions associated with key words relating to Shopping (such as ‘price’, ‘cost’ or ‘change’) into the search box of an Observable List to trawl for names.
Finally, when the appropriate observables have been identified, their definitions – and the actions that modify them – can be revised in accordance with the informal plan for extension of the construal set out above. This is the most technical aspect of the extension process, but is much simplified by the fact that there are pre-existing definitions of the observables to consult, and all such definitions can be readily interpreted empirically by substituting values for their parameters.
The above process can be regarded as having three stages: conception of the transformation of the existing observables that needs to be performed, identification of the names of the relevant observables, and appropriate reconfiguration of the observables, definitions and agency. Of course, other extensions of the basic Shopping construal may require the introduction of features that are not yet represented in the script, but this is not problematic once skills in defining observables of all the different base types have been learnt.
Further illustrations and discussion can be found at [13]. Figure 3 depicts another extension of Shopping in which clicking on the descriptors to the immediate right of the display toggles between posing the questions on the extreme right and supplying their answers. Creating such an extension, as a teacher might in creating an educational resource to scaffold learning life skills, is a relatively straightforward application of basic model-building techniques. A continental variant of Shopping has also been derived.
C. From Shopping to Simple Educational Games
As an educational resource, the variant of the Shopping construal depicted in Figure 3 is more open-ended than many educational programs and games. It serves a role that is somewhat more like an old-fashioned blackboard in that the teacher fashions its content in the stream-of-thought with pedagogical goals in mind. Computational processes are of course involved: images and values are automatically updated and displayed, the environment is at all times open to interactive activities for the learner, and there is scope to record and automate sequences of redefinitions, but the dominant emphasis is on giving support to the teacher’s evolving educational objectives and train of thought.
MoneyMath [16] is an example of a different style of OER. The player is presented with a free form image a few US coins and an item with a price tag attached. There is a button interface through which the player can say whether or not they think they have enough money to buy the item. After each answer, a new question is generated, and the computer keeps score. A Have you enough money? game (HYEM) based on similar principles can be derived from the Shopping construal. This is depicted in Figure 4.
MoneyMath is a game that has been programmed for an explicit teaching purpose. It has a specific intended use; this may not suit the teacher’s needs, but the teacher is not intended to adapt or extend it. When the player’s interaction is restricted to the Canvas interface depicted in Figure 4, the functionality of HYEM is likewise restricted.
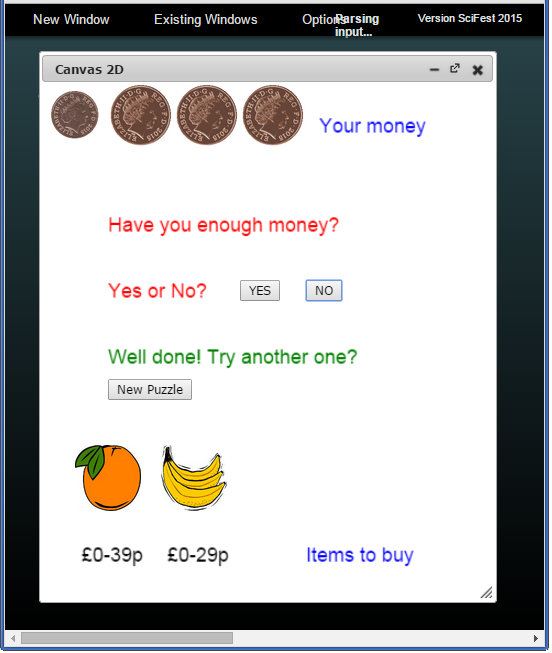
Figure 4: An educational game derived from Shopping
The derivation of the HYEM game from the Shopping construal in Figure 2 follows the same pattern of conception, identification and configuration introduced above.(This derivation can be traced online by following the guidance in section D of the online tutorial resources.) The basic Shopping construal already contains an observable “haveenoughmoney” that registers whether the total spending money is enough to buy the selected items. It also includes an agent that can be invoked to generate a random set of coins for the purse.
As a first approximation to the HYEM game, the contents of the purse can play the role of the coins denoted by ‘Your money’ in Figure 4, and the ‘Items to buy’ can be the first two items selected from the ‘Items for sale’. In this scenario, the layout and logic of the basic Shopping construal can be relatively simply adapted and supplemented with buttons to implement the ‘Yes/No’ and ‘New Puzzle’ protocol to create a prototype for HYEM. Further steps in deriving the version of HYEM depicted in Figure 4 include: adapting an agent that renews the purse to generate a random set of items for sale, restricting ‘Your money’ to the first four coins in the purse, and revising the definition of ‘spendingmoney’ accordingly.
Making construals has virtues as an approach to developing educational games. The intimate connection between the informal commonsense perspective on a game and its realisation as a configuration of observables, dependencies and agency makes it easy to conceive and prototype many variants, stimulating the maker’s imagination and creativity. For instance, at one point in the development, as a result of an error in a filename, certain denominations of coins were not being displayed. This suggests a family of variants of HYEM in which only some of the coins are displayed, and the player can specify ‘yes’, ‘no’ or ‘I don’t know’ as their answer. A further refinement might involve giving players options to disclose the coins until they could give a definitive ‘yes’ or ‘no’ answer, or be challenged to estimate the probability of having enough money.
The emphasis on the player’s experience of a game is also well-suited to the game design objectives. By way of illustration, the observables that define the images of the coins displayed in Figure 4 show ‘heads’ rather than ‘tails’. This hides the numerical values of the coins and differentiates the game from an exercise in mental arithmetic.
IV. CONCLUSION
Disseminating the principles and environments for making construals is a key aim for CONSTRUIT!. Though the principal focus is on schools education, all other varieties of education are within its remit. The Shopping construal is one of several construals that can be accessed online from the Project List at [13]. The Light Box, Hex Colouring and Nim construals incorporate presentations within the MCE that can provide more insight into the issues discussed above. These presentations will be the basis of ‘virtual workshops’ that can serve for learning and teaching how to make construals. An open online course on making construals is also in preparation, and some preliminary resources for this are available via [9]. The evaluation of ‘making construals’ in various ways is being addressed by several collaborative project activities. These include workshops for school teachers and pupils in the UK, Finland and Greece.
ACKNOWLEDGMENTS
We are much indebted to Tim Monks, Nick Pope, Antony Harfield and Joe Butler for their work on the development of the JS-EDEN environment and to Mike Joy for acting as the Coordinator for CONSTRUIT!. This project has been funded with support from the European Commission under the Erasmus+ programme (2014-1-UK01-KA200-001818). This publication reflects the views only of the authors, and the Commission cannot be held responsible for any use which may be made of the information contained therein.
REFERENCES
- D. W. Gooding, Experiment and the Making of Meaning. Springer Science & Business Media, 1990.
- Empirical Modelling, “Empirical Modelling,” 2015. [Online]. Available: http://go.warwick.ac.uk/em. [Accessed: 08-Jul-2015].
- R. Boyatt, M. Beynon, and M. Beynon, “Ghosts of Programming Past, Present and Yet to Come,” in Proceedings of 25th Annual Psychology of Programming Interest Group Annual Conference 2014, 2014, pp. 171–182.
- Empirical Modelling, “Educational technology,” 2011. [Online]. Available: http://www2.warwick.ac.uk/fac/sci/dcs/research/em/applicat ions/educationaltech/. [Accessed: 08-Jul-2015].
- M. Beynon, R. Myers, and A. Harfield, “The Sudoku Experience,” 2008. [Online]. Available: http://www.dcs.warwick.ac.uk/~wmb/sudokuExperience/workshops/. [Accessed: 08-Jul-2015].
- M. Beynon and A. Harfield, “Constructionism through construal by computer,” in Constructionism 2010, 2010.
- S. Gardner, “empublic: oxoGardner1999,” 1999. [Online]. Available: http://empublic.dcs.warwick.ac.uk/projects/oxoGardner1999 /. [Accessed: 08-Jul-2015].
- W. Beynon and M. Joy, “Computer programming for noughts-and-crosses: New frontiers,” in Annual Psychology of Programming Interest Group Conference PPIG’94, 1994, pp. 27–37.
- The CONSTRUIT! Project, “The project,” 2015. [Online]. Available: http://construit.org/. [Accessed: 08-Jul-2015].
- S. Papert, “Mindstorms: children, computers, and powerful ideas,” Jan. 1980.
- Wikipedia, “Open Educational Resources,” 2015. [Online]. Available: https://en.wikipedia.org/wiki/Open_educational_resources.
- DBolical Pty, “Games and mods development for Windows, Linux and Mac -Mod DB,” 2015. [Online]. Available: http://www.moddb.com/.
- The CONSTRUIT! Project, “JS-EDEN,” 2015. [Online]. Available: http://jseden.dcs.warwick.ac.uk/construit/. [Accessed: 08-Jul-2015].
- M. Beynon et al., “Reflections on Making Construals as a New Digital Skill.” submitted for publication, 2015.
- W. James, Essays in radical empiricism (1910). Harvard University Press, 1976.
- Sheppard Software, “Early Math: Enough Money?,” 2015. [Online]. Available: https://www.sheppardsoftware.com/mathgames/earlymath/B PEnoughCoins.htm. [Accessed: 08-Jul-2015].
- D. Popovici, “Money Game,” 2015. [Online]. Available: http://www.math-play.com/money-game.html. [Accessed: 08-Jul-2015].
- Empirical Modelling, “Web-EM-1,” 2005. [Online]. Available: http://www2.warwick.ac.uk/fac/sci/dcs/research/em/publications/web-em/01/. [Accessed: 08-Jul-2015].
- Empirical Modelling, “Eden Language Reference Guide,” 2006. [Online]. Available: http://www2.warwick.ac.uk/fac/sci/dcs/research/em/software/eden/langref/.
